Page 354 - Characterization and Properties of Petroleum Fractions - M.R. Riazi

P1: JDW
AT029-Manual-v7.cls
AT029-Manual
AT029-08
334 CHARACTERIZATION AND PROPERTIES OF PETROLEUM FRACTIONS
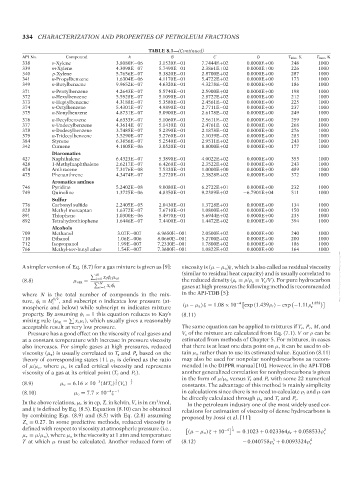
TABLE 8.1—(Continued)
API No. Compound June 22, 2007 14:25 C D T min ,K T max ,K
B
A
338 o-Xylene 3.8080E−06 3.1520E−01 7.7444E+02 0.0000E+00 248 1000
339 m-Xylene 4.3098E−07 5.7490E−01 2.3861E+02 0.0000E+00 226 1000
340 p-Xylene 5.7656E−07 5.3820E−01 2.8700E+02 0.0000E+00 287 1000
341 n-Propylbenzene 1.6304E−06 4.1170E−01 5.4722E+02 0.0000E+00 173 1000
349 n-Butylbenzene 9.9652E−07 4.6320E−01 4.3278E−02 0.0000E+00 186 1000
371 n-Pentylbenzene 4.2643E−07 5.5740E−01 2.5900E+02 0.0000E+00 198 1000
372 n-Hexylbenzene 5.5928E−07 5.1090E−01 2.8722E+02 0.0000E+00 212 1000
373 n-Heptylbenzene 4.3188E−07 5.3580E−01 2.4561E−02 0.0000E+00 225 1000
374 n-Octylbenzene 5.4301E−07 4.9890E−01 2.7711E−02 0.0000E+00 237 1000
375 n-Nonylbenzene 4.8731E−07 5.0900E−01 2.6178E−02 0.0000E+00 249 1000
376 n-Decylbenzene 4.6333E−07 5.1060E−01 2.5611E−02 0.0000E+00 259 1000
377 n-Undecylbenzene 4.3614E−07 5.1410E−01 2.4761E−02 0.0000E+00 268 1000
378 n-Dodecylbenzene 3.7485E−07 5.2390E−01 2.1878E−02 0.0000E+00 276 1000
379 n-Tridecylbenzene 3.5290E−07 5.2760E−01 2.1039E−02 0.0000E+00 283 1000
384 Styrene 6.3856E−07 5.2540E−01 2.9511E+02 0.0000E+00 243 1000
342 Cumene 4.1805E−06 3.0520E−01 8.8000E+02 0.0000E+00 177 1000
Diaromatics
427 Naphthalene 6.4323E−07 5.3890E−01 4.0022E+02 0.0000E+00 353 1000
428 1-Methylnaphthalene 2.6217E−07 6.4260E−01 2.3522E+02 0.0000E+00 243 1000
474 Anthracene 7.3176E−08 7.5320E−01 1.0000E+00 0.0000E+00 489 1000
475 Phenanthrene 4.3474E−07 5.2720E−01 2.3828E+02 0.0000E+00 372 1000
Aromatics amines
746 Pyridine 5.2402E−08 9.0080E−01 6.2722E+01 0.0000E+00 232 1000
749 Quinoline 1.3725E−06 4.8350E−01 9.2389E+02 −6.7901E+04 511 1000
Sulfur
776 Carbonyl sulfide 2.2405E−05 2.0430E−01 1.3728E+03 0.0000E+00 134 1000
828 Methyl mercaptan 1.6372E−07 7.6710E−01 1.0800E+02 0.0000E+00 150 1000
891 Thiophene 1.0300E−06 5.4970E−01 5.6944E+02 0.0000E+00 235 1000
892 Tetrahydrothiophene 1.6446E−07 7.4400E−01 1.4472E+02 0.0000E+00 394 1000
Alcohols
709 Methanol 3.07E−007 6.9650E−001 2.0500E+02 0.0000E+00 240 1000
710 Ethanol 1.06E−006 8.0660E−001 5.2700E+02 0.0000E+00 200 1000
712 Isopropanol 1.99E−007 7.2330E−001 1.7800E+02 0.0000E+00 186 1000
766 Methyl-tert-butyl ether 1.54E−007 7.3600E−001 1.0822E+02 0.0000E+00 164 1000
A simpler version of Eq. (8.7) for a gas mixture is given as [9]: viscosity is (μ − μ a )ξ, which is also called as residual viscosity
(similar to residual heat capacity) and is usually correlated to
N --`,```,`,``````,`,````,```,,-`-`,,`,,`,`,,`---
(8.8) μ om = i=1 x i φ i μ oi the reduced density (ρ r = ρ/ρ c = V c /V). For pure hydrocarbon
N
i=1 x i φ i gases at high pressures the following method is recommended
where N is the total number of compounds in the mix- in the API-TDB [5]:
ture, φ i = M i 1/2 , and subscript o indicates low pressure (at- −4 1.858
mospheric and below) while subscript m indicates mixture (μ − μ a) ξ = 1.08 × 10 exp (1.439ρ r) − exp −1.11ρ r
property. By assuming φ i = 1 this equation reduces to Kay’s (8.11)

mixing rule (μ m = x i μ i ), which usually gives a reasonably
acceptable result at very low pressure. The same equation can be applied to mixtures if T c , P c , M, and
Pressure has a good effect on the viscosity of real gases and V c of the mixture are calculated from Eq. (7.1). V or ρ can be
at a constant temperature with increase in pressure viscosity estimated from methods of Chapter 5. For mixtures, in cases
also increases. For simple gases at high pressures, reduced that there is at least one data point on μ, it can be used to ob-
viscosity (μ r ) is usually correlated to T r and P r based on the tain μ a rather than to use its estimated value. Equation (8.11)
theory of corresponding states [1]. μ r is defined as the ratio may also be used for nonpolar nonhydrocarbons as recom-
of μ/μ c , where μ c is called critical viscosity and represents mended in the DIPPR manual [10]. However, in the API-TDB
viscosity of a gas at its critical point (T c and P c ). another generalized correlation for nonhydrocarbons is given
in the form of μ/μ a versus T r and P r with some 22 numerical
1
2
−3
(8.9) μ c = 6.16 × 10 (MT c ) 2 (V c ) − 3 constants. The advantage of this method is mainly simplicity
−4 −1
(8.10) μ c = 7.7 × 10 ξ in calculations since there is no need to calculate ρ r and μ can
be directly calculated through μ a and T r and P r .
3
In the above relations, μ c is in cp, T c in kelvin, V c is in cm /mol, In the petroleum industry one of the most widely used cor-
and ξ is defined by Eq. (8.5). Equation (8.10) can be obtained relations for estimation of viscosity of dense hydrocarbons is
by combining Eqs. (8.9) and (8.5) with Eq. (2.8) assuming proposed by Jossi et al. [11]:
Z c = 0.27. In some predictive methods, reduced viscosity is
defined with respect to viscosity at atmospheric pressure (i.e., (μ − μ o) ξ + 10 −4
1 4 = 0.1023 + 0.023364ρ r + 0.058533ρ 2
μ r = μ/μ a ), where μ a is the viscosity at 1 atm and temperature r
3
T at which μ must be calculated. Another reduced form of (8.12) − 0.040758ρ + 0.0093324ρ 4
r r

Copyright ASTM International
Provided by IHS Markit under license with ASTM Licensee=International Dealers Demo/2222333001, User=Anggiansah, Erick
No reproduction or networking permitted without license from IHS Not for Resale, 08/26/2021 21:56:35 MDT