Page 88 - Advances in Biomechanics and Tissue Regeneration

5.2 FINITE ELEMENT MODELING OF THE HUMAN BLOOD VESSELS 83

network in which we predicted physiological blood flow and pressure waveforms. This model consists of two parts:
the large arteries (for this study, separately the aorta and the carotid artery) and the small arteries. In both, the
blood flow and pressure are calculated using the incompressible axisymmetric Navier-Stokes equations for a Newto-
nian fluid. A one-dimensional (1D) model is obtained by integrating these equations over the cross-sectional area of
each vessel [24, 25].

5.2.3.3 The Vascular Fractal Network
As commented, the small arteries were modeled as a binary asymmetric-structured tree in which each vessel was
assumed as a straight compliant segment. For computing the fractal tree, the relevant parameters are radii, bifurcation
relationships, asymmetry, area ratios, lengths, and compliance. The vascular network resulted in a series of bifurcating
segments composed of a parent and daughter vessels, as shown in Fig. 5.2. Asymmetry factors α and β guide the scal-
ing of each parent vessel in two daughter vessels according to:

i j i
r i, j ¼ α β r root : (5.2)
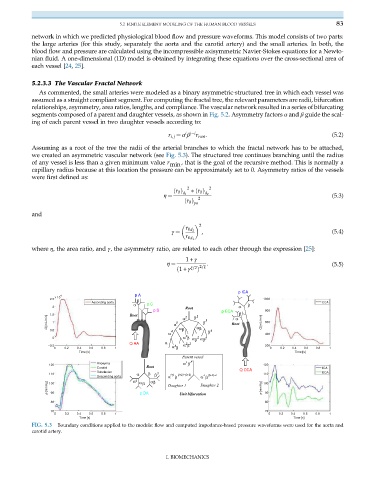
Assuming as a root of the tree the radii of the arterial branches to which the fractal network has to be attached,
we created an asymmetric vascular network (see Fig. 5.3). The structured tree continues branching until the radius
of any vessel is less than a given minimum value r min , that is the goal of the recursive method. This is normally a
capillary radius because at this location the pressure can be approximately set to 0. Asymmetry ratios of the vessels
were first defined as:
2 2
d 1 d 2
ðr 0 Þ + ðr 0 Þ
2
η ¼ (5.3)
ðr 0 Þ pa
and
2

r 0d 2
, (5.4)
γ ¼
r 0d 1
where η, the area ratio, and γ, the asymmetry ratio, are related to each other through the expression [25]:
1+ γ
:
η ¼ (5.5)
ð1+ γ ξ=2 2=ξ
Þ
p ICA
4 p A
x 10
2.5 β 1000
Ascending aorta p C CCA
2 α Root α β
p S p ECA β 800
Q [mL/min] 1.5 1 α 3 α 2 β 2 β 3 Root Q [mL/min] 600
Root
α
0.5 4 α β α β β 4
α 400
2
0 α β α β 2 α β 2
Q AA α 2 2
–0.5 α β α β 200
3
0 0.2 0.4 0.6 0.8 1 0 0.2 0.4 0.6 0.8 1
Time [s] Time [s]
Parent vessel
Anonyma α i β ji
120 120
Carotid Root Q CCA ICA
Subclavian ECA
110 α β β 2 i+j (j+1)−(i+1) i (j+1)−i 110
Descending aorta α β α β
α 2 α β α β 100
p [mmHg] 90 p DA Daughter 1 Daughter 2 p [mmHg] 90
100
Unit bifurcation
80 80
70 70
0 0.2 0.4 0.6 0.8 1 0 0.2 0.4 0.6 0.8 1
Time [s] Time [s]
FIG. 5.3 Boundary conditions applied to the models: flow and computed impedance-based pressure waveforms were used for the aorta and
carotid artery.
I. BIOMECHANICS