Page 241 -

IMPROVING THE SOLUTION 221

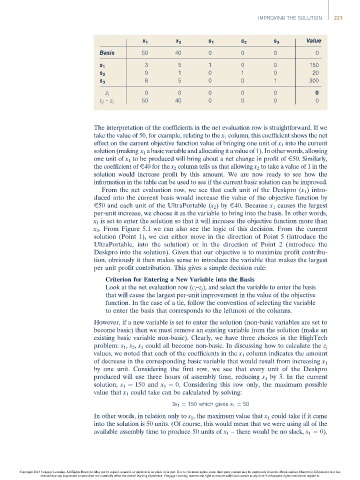
x 1 x 2 s 1 s 2 s 3 Value
Basis 50 40 0 0 0 0
3 5 1 0 0 150
s 1
0 1 0 1 0 20
s 2
8 5 0 0 1 300
s 3
z j 0 0 0 0 0 0
c j –z j 50 40 0 0 0 0

The interpretation of the coefficients in the net evaluation row is straightforward. If we
take the value of 50, for example, relating to the x 1 column, this coefficient shows the net
effect on the current objective function value of bringing one unit of x 1 into the current
solution (making x 1 a basic variable and allocating it a value of 1). In other words, allowing
one unit of x 1 to be produced will bring about a net change in profit of E50. Similarly,
the coefficient of E40 for the x 2 column tells us that allowing x 2 to take a value of 1 in the
solution would increase profit by this amount. We are now ready to see how the
information in the table can be used to see if the current basic solution can be improved.
From the net evaluation row, we see that each unit of the Deskpro (x 1 ) intro-
duced into the current basis would increase the value of the objective function by
E50 and each unit of the UltraPortable (x 2 )by E40. Because x 1 causes the largest
per-unit increase, we choose it as the variable to bring into the basis. In other words,
x 1 is set to enter the solution so that it will increase the objective function more than
x 2 . From Figure 5.1 we can also see the logic of this decision. From the current
solution (Point 1), we can either move in the direction of Point 5 (introduce the
UltraPortable, into the solution) or in the direction of Point 2 (introduce the
Deskpro into the solution). Given that our objective is to maximize profit contribu-
tion, obviously it then makes sense to introduce the variable that makes the largest
per unit profit contribution. This gives a simple decision rule:
Criterion for Entering a New Variable into the Basis
Look at the net evaluation row (c j –z j ), and select the variable to enter the basis
that will cause the largest per-unit improvement in the value of the objective
function. In the case of a tie, follow the convention of selecting the variable
to enter the basis that corresponds to the leftmost of the columns.

However, if a new variable is set to enter the solution (non-basic variables are set to
become basic) then we must remove an existing variable from the solution (make an
existing basic variable non-basic). Clearly, we have three choices in the HighTech
problem: s 1 , s 2 , s 3 could all become non-basic. In discussing how to calculate the z j
values, we noted that each of the coefficients in the x 1 column indicates the amount
of decrease in the corresponding basic variable that would result from increasing x 1
by one unit. Considering the first row, we see that every unit of the Deskpro
produced will use three hours of assembly time, reducing s 1 by 3. In the current
solution, s 1 ¼ 150 and x 1 ¼ 0. Considering this row only, the maximum possible
value that x 1 could take can be calculated by solving:
3x 1 ¼ 150 which gives x 1 ¼ 50

In other words, in relation only to s 1 , the maximum value that x 1 could take if it came
into the solution is 50 units. (Of course, this would mean that we were using all of the
available assembly time to produce 50 units of x 1 – there would be no slack, s 1 ¼ 0).

Copyright 2014 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has
deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.