Page 152 - Analog and Digital Filter Design

149
Highpass Filters

II

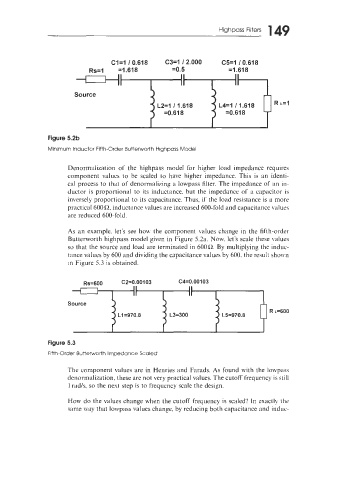
L2=1 11.618 L4=1 11.618 R L=I

Denormalization of the highpass model for higher load impedance requires
component values to be scaled to have higher impedance. This is an identi-
cal process to that of denormalizing a lowpass filter. The impedance of an in-
ductor is proportional to its inductance. but the impedance of a capacitor is
inversely proportional to its capacitance. Thus, if the load resistance is a more
practical 600R, inductance values are increased 600-fold and capacitance values
are reduced 600-fold.

.4s an example. let's see hoM the component \dues change in the fifth-order
Butterworth highpass model given in Figure 5.2a. Now. let's scale these values
so that the source and load are terminated in 600Q. By multiplying the induc-
tance values by 600 and dividing the capacitance values by 600. the result shonn
in Figure 5.3 is obtained.

Rs=600 C2=0.00103 C4=0.00103

Source
R ~=600
L1=970.8 L3=300 L5=970.8

Figure 5.3
Fifth-Order Butterworth Impedance Scaled

The component values are in Henries and Farads. As found with the loivpass
denornialization, these are not very practical values. The cutoff frequency is still
1 rad/s, so the next step is to frequency scale the design.

How do the values change when the cutoff frequency is scaled! In exactly the
same way that lowpass values change, by reducing both capacitance and induc-