Page 32 - Analytical Electrochemistry 2d Ed - Jospeh Wang

1-2 FARADAIC PROCESSES 17

same in both directions. A, known as the frequency factor, is given as a simple
0
function of the Boltzmann constant k and the Planck constant, h:

k T
0
A ˆ 1-35†
h
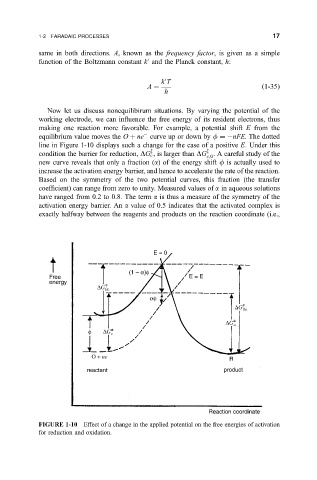
Now let us discuss nonequilibirum situations. By varying the potential of the
working electrode, we can in¯uence the free energy of its resident electrons, thus
making one reaction more favorable. For example, a potential shift E from the
equilibrium value moves the O ‡ ne curve up or down by f ˆ nFE. The dotted

line in Figure 1-10displays such a change for the case of a positive E. Under this
z
z
condition the barrier for reduction, DG c , is larger than DG . A careful study of the
c;0
new curve reveals that only a fraction (a) of the energy shift f is actually used to
increase the activation energy barrier, and hence to accelerate the rate of the reaction.
Based on the symmetry of the two potential curves, this fraction (the transfer
coef®cient) can range from zero to unity. Measured values of a in aqueous solutions
have ranged from 0.2 to 0.8. The term a is thus a measure of the symmetry of the
activation energy barrier. An a value of 0.5 indicates that the activated complex is
exactly halfway between the reagents and products on the reaction coordinate (i.e.,

FIGURE 1-10 Effect of a change in the applied potential on the free energies of activation
for reduction and oxidation.