Page 164 - Applied Numerical Methods Using MATLAB

FOURIER TRANSFORM 153

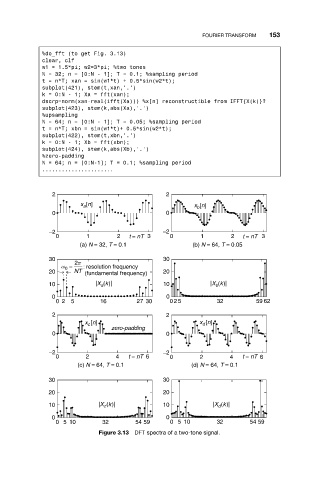
%do_fft (to get Fig. 3.13)
clear, clf
w1 = 1.5*pi; w2=3*pi; %two tones
N = 32; n = [0:N - 1]; T = 0.1; %sampling period
t = n*T; xan = sin(w1*t) + 0.5*sin(w2*t);
subplot(421), stem(t,xan,’.’)
k = 0:N - 1; Xa = fft(xan);
dscrp=norm(xan-real(ifft(Xa))) %x[n] reconstructible from IFFT{X(k)}?
subplot(423), stem(k,abs(Xa),’.’)
%upsampling
N = 64; n = [0:N - 1]; T = 0.05; %sampling period
t = n*T; xbn = sin(w1*t)+ 0.5*sin(w2*t);
subplot(422), stem(t,xbn,’.’)
k = 0:N - 1; Xb = fft(xbn);
subplot(424), stem(k,abs(Xb),’.’)
%zero-padding
N = 64; n = [0:N-1]; T = 0.1; %sampling period
......................

2 2
x [n] x [n]
a
b
0 0
−2 −2
0 1 2 t = nT 3 0 1 2 t = nT 3
(a) N = 32, T = 0.1 (b) N = 64, T = 0.05
30 30
= 2p
w 0 : resolution frequency
20 NT (fundamental frequency) 20
10 |X (k)| 10 |X (k)|
b
a
0 0
02 5 16 27 30 0 2 5 32 59 62
2 2
x [n] x [n]
d
c
zero-padding
0 0
−2 −2
0 2 4 t = nT 6 0 2 4 t = nT 6
(c) N = 64, T = 0.1 (d) N = 64, T = 0.1

30 30
20 20
10 |X (k)| 10 |X (k)|
d
c
0 0
0 5 10 32 54 59 0 5 10 32 54 59
Figure 3.13 DFT spectra of a two-tone signal.