Page 345 - Automotive Engineering Powertrain Chassis System and Vehicle Body

CHAP TER 1 1. 1 Tyre characteristics and vehicle handling and stability

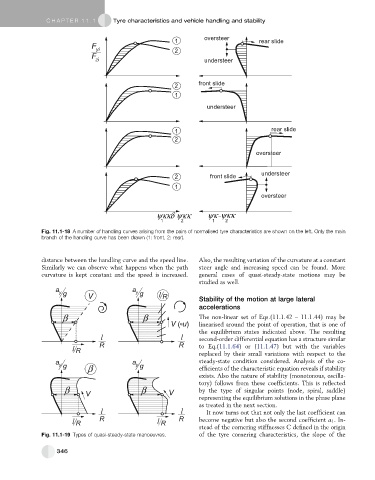
Fig. 11.1-18 A number of handling curves arising from the pairs of normalised tyre characteristics are shown on the left. Only the main
branch of the handling curve has been drawn (1: front, 2: rear).

distance between the handling curve and the speed line. Also, the resulting variation of the curvature at a constant
Similarly we can observe what happens when the path steer angle and increasing speed can be found. More
curvature is kept constant and the speed is increased. general cases of quasi-steady-state motions may be
studied as well.

Stability of the motion at large lateral
accelerations
The non-linear set of Eqs.(11.1.42 – 11.1.44) may be
linearised around the point of operation, that is one of
the equilibrium states indicated above. The resulting
second-order differential equation has a structure similar
to Eq.(11.1.64)or(11.1.47) but with the variables
replaced by their small variations with respect to the
steady-state condition considered. Analysis of the co-
efficients of the characteristic equation reveals if stability
exists. Also the nature of stability (monotonous, oscilla-
tory) follows from these coefficients. This is reflected
by the type of singular points (node, spiral, saddle)
representing the equilibrium solutions in the phase plane
as treated in the next section.
It now turns out that not only the last coefficient can
become negative but also the second coefficient a 1 . In-
stead of the cornering stiffnesses C defined in the origin
Fig. 11.1-19 Types of quasi-steady-state manoeuvres. of the tyre cornering characteristics, the slope of the

346