Page 175 - Basics of MATLAB and Beyond

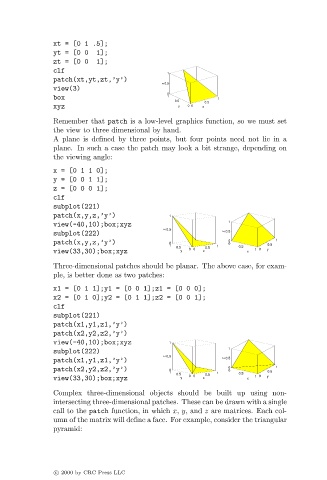
xt = [0 1 .5];
yt=[00 1];
zt=[00 1];
clf
1
patch(xt,yt,zt,’y’)
0.5
z
view(3)
0
box 1 1
0.5
0.5
xyz y 0 0 x
Remember that patch is a low-level graphics function, so we must set
the view to three dimensional by hand.
A plane is defined by three points, but four points need not lie in a
plane. In such a case the patch may look a bit strange, depending on
the viewing angle:
x=[0110];
y=[0011];
z=[0001];
clf
subplot(221)
patch(x,y,z,’y’) 1
1
view(-40,10);box;xyz
z 0.5
subplot(222) z 0.5
patch(x,y,z,’y’) 0 0 0 1
1 1 0.5 0.5
0.5 0 0.5
view(33,30);box;xyz y 0 x x 1 0 y
Three-dimensional patches should be planar. The above case, for exam-
ple, is better done as two patches:
x1 = [0 1 1];y1 = [0 0 1];z1 = [0 0 0];
x2 = [0 1 0];y2 = [0 1 1];z2 = [0 0 1];
clf
subplot(221)
patch(x1,y1,z1,’y’)
patch(x2,y2,z2,’y’)
view(-40,10);box;xyz 1
subplot(222) 1
z 0.5
patch(x1,y1,z1,’y’) z 0.5
patch(x2,y2,z2,’y’) 0 0 0 1
1 0.5 0.5 1 0.5 0.5
view(33,30);box;xyz y 0 0 x x 1 0 y
Complex three-dimensional objects should be built up using non-
intersecting three-dimensional patches. These can be drawn with a single
call to the patch function, in which x, y, and z are matrices. Each col-
umn of the matrix will define a face. For example, consider the triangular
pyramid:

c 2000 by CRC Press LLC