Page 185 - Biomedical Engineering and Design Handbook Volume 1, Fundamentals

162 BIOMECHANICS OF THE HUMAN BODY

7.3 BODY-SEGMENTAL DYNAMICS

7.3.1 Generalized Coordinates and Degrees of Freedom
The minimum number of coordinates needed to specify the position and orientation of a body in
space is the set of generalized coordinates for the body. The number of degrees of freedom (dof) of
the body is equal to the number of generalized coordinates minus the number of kinematic con-
straints acting on the body at the instant under consideration (Kane and Levinson, 1985). For exam-
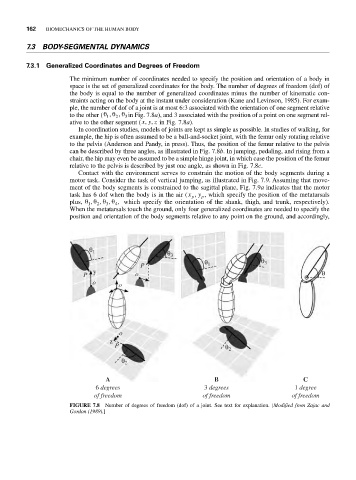
ple, the number of dof of a joint is at most 6:3 associated with the orientation of one segment relative
to the other ( θθ θ, 2 , 3 in Fig. 7.8a), and 3 associated with the position of a point on one segment rel-
1
ative to the other segment ( xy z,, in Fig. 7.8a).
In coordination studies, models of joints are kept as simple as possible. In studies of walking, for
example, the hip is often assumed to be a ball-and-socket joint, with the femur only rotating relative
to the pelvis (Anderson and Pandy, in press). Thus, the position of the femur relative to the pelvis
can be described by three angles, as illustrated in Fig. 7.8b. In jumping, pedaling, and rising from a
chair, the hip may even be assumed to be a simple hinge joint, in which case the position of the femur
relative to the pelvis is described by just one angle, as shown in Fig. 7.8c.
Contact with the environment serves to constrain the motion of the body segments during a
motor task. Consider the task of vertical jumping, as illustrated in Fig. 7.9. Assuming that move-
ment of the body segments is constrained to the sagittal plane, Fig. 7.9a indicates that the motor
task has 6 dof when the body is in the air (x , y p , which specify the position of the metatarsals
p
plus, θθ θ θ, 2 , 3 , 4 , which specify the orientation of the shank, thigh, and trunk, respectively).
1
When the metatarsals touch the ground, only four generalized coordinates are needed to specify the
position and orientation of the body segments relative to any point on the ground, and accordingly,

θ 1 θ
3
θ θ 3
P 1
y θ
P o
o o

o
z
P θ 2
θ 2

A B C
6 degrees 3 degrees 1 degree
of freedom of freedom of freedom
FIGURE 7.8 Number of degrees of freedom (dof) of a joint. See text for explanation. [Modified from Zajac and
Gordon (1989).]