Page 186 - Biomedical Engineering and Design Handbook Volume 1, Fundamentals

BIOMECHANICS OF THE MUSCULOSKELETAL SYSTEM 163

θ 4

θ
θ 3 4
θ 4

θ 2 θ 3
θ 3
θ 1
y y θ y
P (x , y ) 2
P
P
x x θ 1 x θ 2
A B C
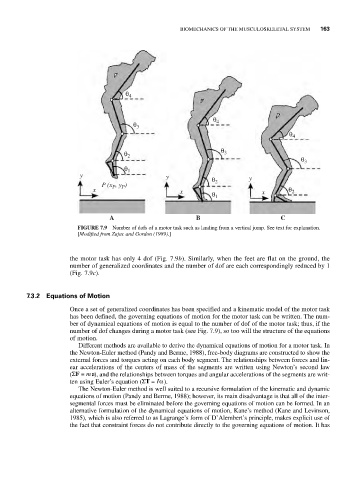
FIGURE 7.9 Number of dofs of a motor task such as landing from a vertical jump. See text for explanation.
[Modified from Zajac and Gordon (1989).]

the motor task has only 4 dof (Fig. 7.9b). Similarly, when the feet are flat on the ground, the
number of generalized coordinates and the number of dof are each correspondingly reduced by 1
(Fig. 7.9c).

7.3.2 Equations of Motion
Once a set of generalized coordinates has been specified and a kinematic model of the motor task
has been defined, the governing equations of motion for the motor task can be written. The num-
ber of dynamical equations of motion is equal to the number of dof of the motor task; thus, if the
number of dof changes during a motor task (see Fig. 7.9), so too will the structure of the equations
of motion.
Different methods are available to derive the dynamical equations of motion for a motor task. In
the Newton-Euler method (Pandy and Berme, 1988), free-body diagrams are constructed to show the
external forces and torques acting on each body segment. The relationships between forces and lin-
ear accelerations of the centers of mass of the segments are written using Newton’s second law
(ΣF = m a ), and the relationships between torques and angular accelerations of the segments are writ-
ten using Euler’s equation (ΣT = Iα ).
The Newton-Euler method is well suited to a recursive formulation of the kinematic and dynamic
equations of motion (Pandy and Berme, 1988); however, its main disadvantage is that all of the inter-
segmental forces must be eliminated before the governing equations of motion can be formed. In an
alternative formulation of the dynamical equations of motion, Kane’s method (Kane and Levinson,
1985), which is also referred to as Lagrange’s form of D’Alembert’s principle, makes explicit use of
the fact that constraint forces do not contribute directly to the governing equations of motion. It has