Page 199 - Biomedical Engineering and Design Handbook Volume 1, Fundamentals

176 BIOMECHANICS OF THE HUMAN BODY

Myosin head

Actin
(+) (–)
Head dissociates
1 Nucleotide
ATP from filament

Head pivots and binds
2 Hydrolysis a new actin subunit

ADP • P i

Head pivots and moves
release
3 P i
P i filament (power stroke)

4 ADP release
ADP

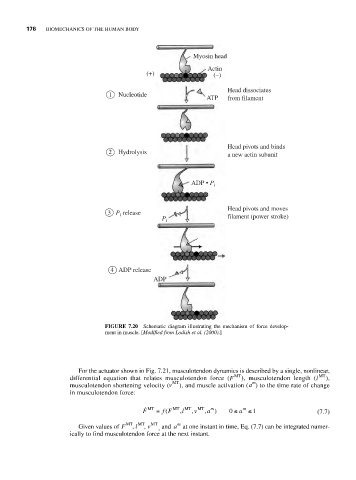
FIGURE 7.20 Schematic diagram illustrating the mechanism of force develop-
ment in muscle. [Modified from Lodish et al. (2000).]

For the actuator shown in Fig. 7.21, musculotendon dynamics is described by a single, nonlinear,
MT MT
differential equation that relates musculotendon force (F ), musculotendon length (l ),
musculotendon shortening velocity (v MT ), and muscle activation (a m ) to the time rate of change
in musculotendon force:
m
F MT = f F ( MT l , MT v , MT a , m ) 0 ≤ a ≤1 (7.7)
Given values of F MT l , MT v , MT , and a m at one instant in time, Eq. (7.7) can be integrated numer-
ically to find musculotendon force at the next instant.