Page 131 - Cam Design Handbook
P. 131
THB5 8/15/03 1:52 PM Page 119
CAM MOTION SYNTHESIS USING SPLINE FUNCTIONS 119
2
1
Displacement (cm)
0
Splines
Polynomials
Constraint
–1
0 90 180 270
Cam rotation angle (deg.)
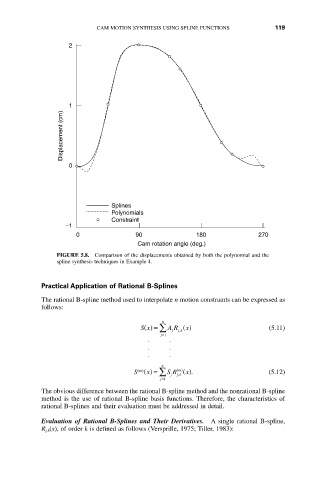
FIGURE 5.8. Comparison of the displacements obtained by both the polynomial and the
spline synthesis techniques in Example 4.
Practical Application of Rational B-Splines
The rational B-spline method used to interpolate n motion constraints can be expressed as
follows:
n
Sx () = Â A R () (5.11)
x
j j k ,
j=1
. .
. .
. .
n
S () = Â S R (). (5.12)
()
m
m
()
x
x
j k ,
j
j=1
The obvious difference between the rational B-spline method and the nonrational B-spline
method is the use of rational B-spline basis functions. Therefore, the characteristics of
rational B-splines and their evaluation must be addressed in detail.
Evaluation of Rational B-Splines and Their Derivatives. A single rational B-spline,
R j,k(x), of order k is defined as follows (Versprille, 1975; Tiller, 1983):