Page 132 - Cam Design Handbook

THB5 8/15/03 1:52 PM Page 120

120 CAM DESIGN HANDBOOK

4

2
Velocity (cm/rad)

0

Splines
Polynomials
Constraints
–2
0 90 180 270
Cam rotation angle (deg.)
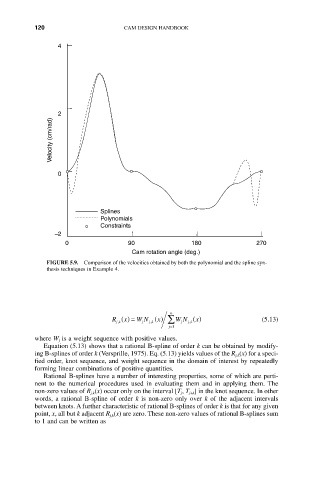
FIGURE 5.9. Comparison of the velocities obtained by both the polynomial and the spline syn-
thesis techniques in Example 4.

n
x Â
x
x
R () = W N () W N () (5.13)
jk ,
jk ,
j
jk ,
j
j=1
where W j is a weight sequence with positive values.
Equation (5.13) shows that a rational B-spline of order k can be obtained by modify-
ing B-splines of order k (Versprille, 1975). Eq. (5.13) yields values of the R j,k (x) for a speci-
fied order, knot sequence, and weight sequence in the domain of interest by repeatedly
forming linear combinations of positive quantities.
Rational B-splines have a number of interesting properties, some of which are perti-
nent to the numerical procedures used in evaluating them and in applying them. The
non-zero values of R j,k(x) occur only on the interval [T j, T j+k] in the knot sequence. In other
words, a rational B-spline of order k is non-zero only over k of the adjacent intervals
between knots. A further characteristic of rational B-splines of order k is that for any given
point, x, all but k adjacent R j,k(x) are zero. These non-zero values of rational B-splines sum
to 1 and can be written as