Page 74 - Chalcogenide Glasses for Infrared Optics

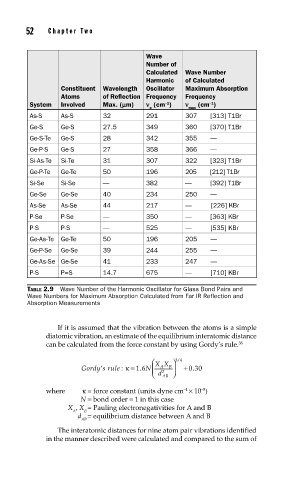
52 Cha pte r T w o

Wave
Number of
Calculated Wave Number
Harmonic of Calculated
Constituent Wavelength Oscillator Maximum Absorption
Atoms of Reflection Frequency Frequency
–1
System Involved Max. (mm) n (cm ) n (cm )
–1
o max
As-S As-S 32 291 307 [313] T1Br
Ge-S Ge-S 27.5 349 360 [370] T1Br
Ge-S-Te Ge-S 28 342 355 —
Ge-P-S Ge-S 27 358 366 —
Si-As-Te Si-Te 31 307 322 [323] T1Br
Ge-P-Te Ge-Te 50 196 205 [212] T1Br
Si-Se Si-Se — 382 — [392] T1Br
Ge-Se Ge-Se 40 234 250 —
As-Se As-Se 44 217 — [226] KBr
P-Se P-Se — 350 — [363] KBr
P-S P-S — 525 — [535] KBr
Ge-As-Te Ge-Te 50 196 205 —
Ge-P-Se Ge-Se 39 244 255 —
Ge-As-Se Ge-Se 41 233 247 —
P-S P=S 14.7 675 — [710] KBr

TABLE 2.9 Wave Number of the Harmonic Oscillator for Glass Bond Pairs and
Wave Numbers for Maximum Absorption Calculated from Far IR Reflection and
Absorption Measurements

If it is assumed that the vibration between the atoms is a simple
diatomic vibration, an estimate of the equilibrium interatomic distance
can be calculated from the force constant by using Gordy’s rule. 38

 XX  34
/
.
Gordy s rule : κ= 16 N  A B  + . 030
’
2
 d AB 
–5
–1
where κ = force constant (units dyne cm × 10 )
N = bond order = 1 in this case
X , X = Pauling electronegativities for A and B
A B
d = equilibrium distance between A and B
AB
The interatomic distances for nine atom pair vibrations identified
in the manner described were calculated and compared to the sum of