Page 75 - Chalcogenide Glasses for Infrared Optics

Chalcogenide Glasses 53

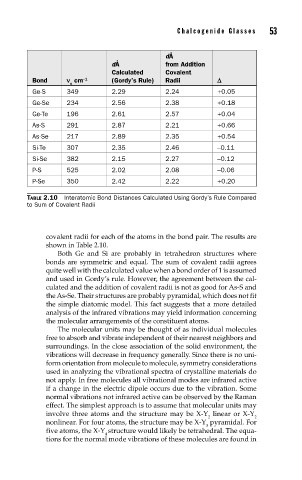
dÅ
dÅ from Addition
Calculated Covalent
Bond n cm –1 (Gordy’s Rule) Radii D
o
Ge-S 349 2.29 2.24 +0.05
Ge-Se 234 2.56 2.38 +0.18
Ge-Te 196 2.61 2.57 +0.04
As-S 291 2.87 2.21 +0.66
As-Se 217 2.89 2.35 +0.54
Si-Te 307 2.35 2.46 –0.11
Si-Se 382 2.15 2.27 –0.12
P-S 525 2.02 2.08 –0.06
P-Se 350 2.42 2.22 +0.20

TABLE 2.10 Interatomic Bond Distances Calculated Using Gordy’s Rule Compared
to Sum of Covalent Radii

covalent radii for each of the atoms in the bond pair. The results are
shown in Table 2.10.
Both Ge and Si are probably in tetrahedron structures where
bonds are symmetric and equal. The sum of covalent radii agrees
quite well with the calculated value when a bond order of 1 is assumed
and used in Gordy’s rule. However, the agreement between the cal-
culated and the addition of covalent radii is not as good for As-S and
the As-Se. Their structures are probably pyramidal, which does not fit
the simple diatomic model. This fact suggests that a more detailed
analysis of the infrared vibrations may yield information concerning
the molecular arrangements of the constituent atoms.
The molecular units may be thought of as individual molecules
free to absorb and vibrate independent of their nearest neighbors and
surroundings. In the close association of the solid environment, the
vibrations will decrease in frequency generally. Since there is no uni-
form orientation from molecule to molecule, symmetry considerations
used in analyzing the vibrational spectra of crystalline materials do
not apply. In free molecules all vibrational modes are infrared active
if a change in the electric dipole occurs due to the vibration. Some
normal vibrations not infrared active can be observed by the Raman
effect. The simplest approach is to assume that molecular units may
involve three atoms and the structure may be X-Y linear or X-Y
2 2
nonlinear. For four atoms, the structure may be X-Y pyramidal. For
3
five atoms, the X-Y structure would likely be tetrahedral. The equa-
4
tions for the normal mode vibrations of these molecules are found in