Page 295 - Classification Parameter Estimation & State Estimation An Engg Approach Using MATLAB

284 STATE ESTIMATION IN PRACTICE

x 10 –6 minimum eigenvalue of C(i|i)
2 15 measurements
10
0
5
0
–2
–5
–4 –10
0 50 100 150 200
–6 0.2 estimation errors
0.1
–8
0
–10
–0.1
–12 –0.2
0 50 100 150 200 0 50 100 150 200
i i
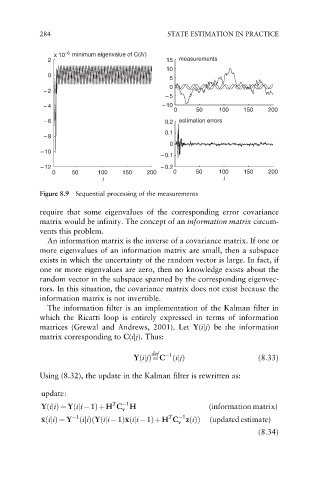
Figure 8.9 Sequential processing of the measurements

require that some eigenvalues of the corresponding error covariance
matrix would be infinity. The concept of an information matrix circum-
vents this problem.
An information matrix is the inverse of a covariance matrix. If one or
more eigenvalues of an information matrix are small, then a subspace
exists in which the uncertainty of the random vector is large. In fact, if
one or more eigenvalues are zero, then no knowledge exists about the
random vector in the subspace spanned by the corresponding eigenvec-
tors. In this situation, the covariance matrix does not exist because the
information matrix is not invertible.
The information filter is an implementation of the Kalman filter in
which the Ricatti loop is entirely expressed in terms of information
matrices (Grewal and Andrews, 2001). Let Y(ijj) be the information
matrix corresponding to C(ijj). Thus:

def 1
YðijjÞ¼C ðijjÞ ð8:33Þ

Using (8.32), the update in the Kalman filter is rewritten as:

update:
T
1
YðijiÞ¼ Yðiji 1ÞþH C H (information matrix)
v
1 T 1
x
x xðijiÞ¼ Y ðijiÞðYðiji 1Þ xðiji 1ÞþH C zðiÞÞ (updated estimate)
v
ð8:34Þ