Page 297 - Classification Parameter Estimation & State Estimation An Engg Approach Using MATLAB

286 STATE ESTIMATION IN PRACTICE

available. However, the information matrix cannot represent a situa-
tion where states are known precisely, i.e. without uncertainty.
Typically, such a situation occurs when the system (F, G)is not
controllable.
The information filter also offers the possibility to define a stochastic
observability criterion. For that purpose, consider the system without
1
1 T
process noise. In that case, Y(i þ 1ji) ¼ (F ) Y(iji)F . Starting with
complete uncertainty, i.e. Y(0j 1) ¼ 0, the prediction information at
time i is found by iterative application of (8.34):
i
X j j
1 T T 1 1
Yðiji 1Þ¼ ðF Þ H C HF ð8:38Þ
v
j¼0
Note the similarity of this expression with the observability Grammian
given in (8.17). The only difference is the information matrix C 1 which
v
weighs the importance of the measurements. Clearly, if for some i all
eigenvalues of Y(iji 1) are positive, then the measurements have pro-
vided information to all states.

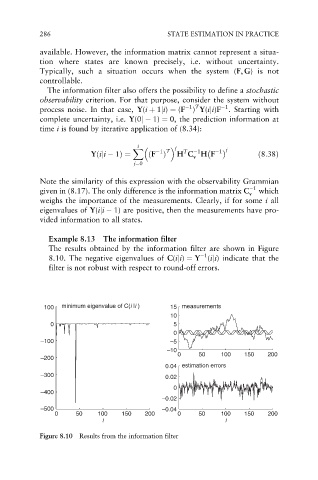
Example 8.13 The information filter
The results obtained by the information filter are shown in Figure
1
8.10. The negative eigenvalues of C(iji) ¼ Y (iji) indicate that the
filter is not robust with respect to round-off errors.

100 minimum eigenvalue of C(i |i ) 15 measurements
10
0 5
0
–100 –5
–10
0 50 100 150 200
–200
0.04 estimation errors
–300 0.02
0
–400
–0.02
–500 –0.04
0 50 100 150 200 0 50 100 150 200
i i
Figure 8.10 Results from the information filter