Page 302 - Classification Parameter Estimation & State Estimation An Engg Approach Using MATLAB

COMPUTATIONAL ISSUES 291

estimation error should be inversely proportional to the number of
observations.

8.3.5 Comparison

In the preceding sections, five different implementations are discussed
which are all mathematically equivalent. However, different implemen-
tations have different sensitivities to round-off errors and different com-
putational cost.
Table 8.1 provides an overview of the cost expressed in the number
of operations required for a single iteration. The table assumes a time
1
T
invariant system so that terms like H C H can be reused. Furthermore,
v
the numbers are based on a straightforward MATLAB implementation with-
out optimization with respect to computational cost. Special code that
exploits the symmetry of covariance matrices can lower the number of
operations a little. The computational efficiency of the square root filter
can be improved by consistently maintaining the triangular structure of the
matrices. (In the current implementation, the triangular structure is lost
during the update, but is regained by the QR factorization.)
A quantitative, general analysis of the sensitivities of the various
implementations to round-off errors is difficult. However, Table 8.1
gives an indication. The table shows the results of an experiment that
relates to the system described in Example 8.10. For each implementation,

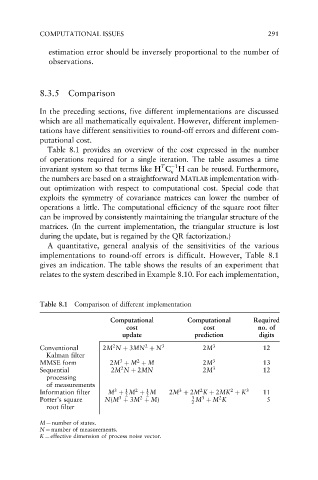
Table 8.1 Comparison of different implementation

Computational Computational Required
cost cost no. of
update prediction digits
2
2
Conventional 2M N þ 3MN þ N 3 2M 3 12
Kalman filter
2
3
MMSE form 2M þ M þ M 2M 3 13
2
Sequential 2M N þ 2MN 2M 3 12
processing
of measurements
2
2
1
3
2
3
1
Information filter M þ M þ M 2M þ 2M K þ 2MK þ K 3 11
2
2
3
2
3
2
Potter’s square N(M þ 3M þ M) 3 2 M þ M K 5
root filter
M ¼ number of states.
N ¼ number of measurements.
K ¼ effective dimension of process noise vector.