Page 303 - Classification Parameter Estimation & State Estimation An Engg Approach Using MATLAB

292 STATE ESTIMATION IN PRACTICE

10 –6 minimum eigenvalue of C(i |i ) 15 measurements
10
5
0
10 –7 –5
–10
0 50 100 150 200
0.04 estimation errors
10 –8 0.02
0
–0.02
10 –9 –0.04
10 0 10 1 10 2 0 50 100 150 200
i i
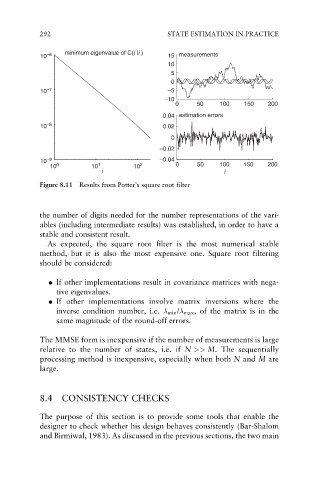
Figure 8.11 Results from Potter’s square root filter

the number of digits needed for the number representations of the vari-
ables (including intermediate results) was established, in order to have a
stable and consistent result.
As expected, the square root filter is the most numerical stable
method, but it is also the most expensive one. Square root filtering
should be considered:

. If other implementations result in covariance matrices with nega-
tive eigenvalues.
. If other implementations involve matrix inversions where the
inverse condition number, i.e. min / max , of the matrix is in the
same magnitude of the round-off errors.

The MMSE form is inexpensive if the number of measurements is large
relative to the number of states, i.e. if N >> M. The sequentially
processing method is inexpensive, especially when both N and M are
large.

8.4 CONSISTENCY CHECKS

The purpose of this section is to provide some tools that enable the
designer to check whether his design behaves consistently (Bar-Shalom
and Birmiwal, 1983). As discussed in the previous sections, the two main