Page 307 - Classification Parameter Estimation & State Estimation An Engg Approach Using MATLAB

296 STATE ESTIMATION IN PRACTICE

true
first state estimate 5 error first state 10 nees
10
0 0 5

–10
–5 0
0 50 100 0 50 100 0 50 100
second state 5 error second state 8 nis
10
6
0 0 4
2
–10
–5 0
0 50 100 0 50 100 0 50 100
i
10 measurements 4 innovations 10 periodogram
5 2
0 0 5
–5 –2
–10 –4 0
0 50 100 0 50 100 0 50 100
i i k

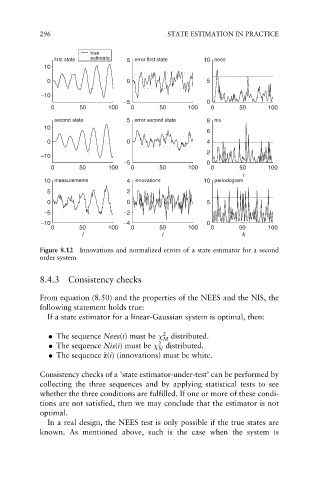
Figure 8.12 Innovations and normalized errors of a state estimator for a second
order system

8.4.3 Consistency checks

From equation (8.50) and the properties of the NEES and the NIS, the
following statement holds true:
If a state estimator for a linear-Gaussian system is optimal, then:

. The sequence Nees(i) must be 2 distributed.
M
2
. The sequence Nis(i) must be distributed.
N
. The sequence ~ z(i) (innovations) must be white.
z
Consistency checks of a ’state estimator-under-test’ can be performed by
collecting the three sequences and by applying statistical tests to see
whether the three conditions are fulfilled. If one or more of these condi-
tions are not satisfied, then we may conclude that the estimator is not
optimal.
In a real design, the NEES test is only possible if the true states are
known. As mentioned above, such is the case when the system is