Page 310 - Classification Parameter Estimation & State Estimation An Engg Approach Using MATLAB

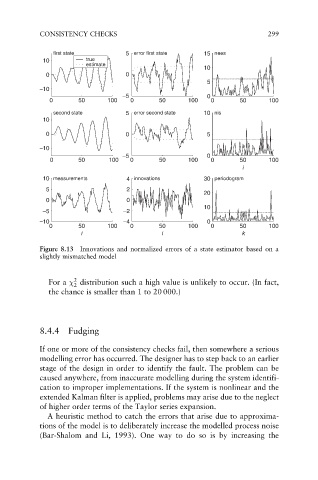
CONSISTENCY CHECKS 299

first state 5 error first state 15 nees
10 true
estimate
10
0 0
5
–10
–5 0
0 50 100 0 50 100 0 50 100
second state 5 error second state 10 nis
10
0 0 5

–10
–5 0
0 50 100 0 50 100 0 50 100
i
10 measurements 4 innovations 30 periodogram
5 2
20
0 0
10
–5 –2
–10 –4 0
0 50 100 0 50 100 0 50 100
i i k

Figure 8.13 Innovations and normalized errors of a state estimator based on a
slightly mismatched model

2
For a distribution such a high value is unlikely to occur. (In fact,
2
the chance is smaller than 1 to 20 000.)

8.4.4 Fudging

If one or more of the consistency checks fail, then somewhere a serious
modelling error has occurred. The designer has to step back to an earlier
stage of the design in order to identify the fault. The problem can be
caused anywhere, from inaccurate modelling during the system identifi-
cation to improper implementations. If the system is nonlinear and the
extended Kalman filter is applied, problems may arise due to the neglect
of higher order terms of the Taylor series expansion.
A heuristic method to catch the errors that arise due to approxima-
tions of the model is to deliberately increase the modelled process noise
(Bar-Shalom and Li, 1993). One way to do so is by increasing the