Page 338 - Classification Parameter Estimation & State Estimation An Engg Approach Using MATLAB

TIME-OF-FLIGHT ESTIMATION OF AN ACOUSTIC TONE BURST 327

observed waveform

8 8.5 9 9.5 10 t (ms)
matched filtering τ
match

8 8.5 9 9.5 10 t (ms)
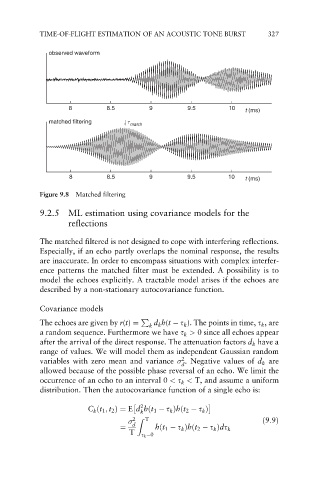
Figure 9.8 Matched filtering

9.2.5 ML estimation using covariance models for the
reflections

The matched filtered is not designed to cope with interfering reflections.
Especially, if an echo partly overlaps the nominal response, the results
are inaccurate. In order to encompass situations with complex interfer-
ence patterns the matched filter must be extended. A possibility is to
model the echoes explicitly. A tractable model arises if the echoes are
described by a non-stationary autocovariance function.

Covariance models
P
The echoes are given by r(t) ¼ k d k h(t t k ). The points in time, t k , are
a random sequence. Furthermore we have t k > 0 since all echoes appear
after the arrival of the direct response. The attenuation factors d k have a
range of values. We will model them as independent Gaussian random
2
variables with zero mean and variance . Negative values of d k are
d
allowed because of the possible phase reversal of an echo. We limit the
occurrence of an echo to an interval 0 < t k < T, and assume a uniform
distribution. Then the autocovariance function of a single echo is:

2

C k ðt 1 ; t 2 Þ¼ E d hðt 1 t k Þhðt 2 t k Þ
k
2 Z T ð9:9Þ
¼ d hðt 1 t k Þhðt 2 t k Þdt k
T t k ¼0