Page 25 - Complementarity and Variational Inequalities in Electronics

The Convex Subdifferential Relation Chapter | 2 15

∗
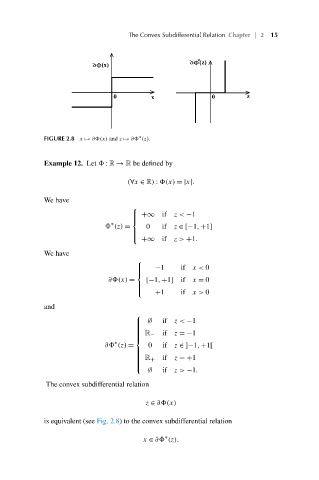
FIGURE 2.8 x ð ∂ (x) and z ð ∂ (z).

Example 12. Let : R → R be defined by

(∀x ∈ R) : (x) =|x|.

We have
⎧
⎪ +∞ if z< −1
⎪
⎨
∗
(z) = 0 if z ∈[−1,+1]
⎪
⎪
+∞ if z> +1.
⎩
We have
⎧
−1 if x< 0
⎪
⎪
⎨
∂ (x) = [−1,+1] if x = 0
⎪
⎪
+1 if x> 0
⎩
and
⎧
⎪ ∅ if z< −1
⎪
⎪
if z =−1
⎪
⎪
⎪ R −
⎪
⎨
∗
∂ (z) = 0 if z ∈]−1,+1[
⎪
⎪
if z =+1
⎪
⎪ R +
⎪
⎪
⎪
⎩
∅ if z> −1.
The convex subdifferential relation
z ∈ ∂ (x)
is equivalent (see Fig. 2.8) to the convex subdifferential relation
∗
x ∈ ∂ (z).