Page 169 - Computational Modeling in Biomedical Engineering and Medical Physics

158 Computational Modeling in Biomedical Engineering and Medical Physics

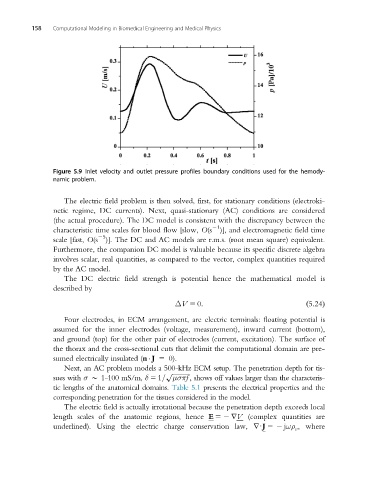
Figure 5.9 Inlet velocity and outlet pressure profiles boundary conditions used for the hemody-
namic problem.

The electric field problem is then solved, first, for stationary conditions (electroki-
netic regime, DC currents). Next, quasi-stationary (AC) conditions are considered
(the actual procedure). The DC model is consistent with the discrepancy between the
characteristic time scales for blood flow [slow, O(s 21 )], and electromagnetic field time
25
scale [fast, O(s )]. The DC and AC models are r.m.s. (root mean square) equivalent.
Furthermore, the companion DC model is valuable because its specific discrete algebra
involves scalar, real quantities, as compared to the vector, complex quantities required
by the AC model.
The DC electric field strength is potential hence the mathematical model is
described by

ΔV 5 0: ð5:24Þ

Four electrodes, in ECM arrangement, are electric terminals: floating potential is
assumed for the inner electrodes (voltage, measurement), inward current (bottom),
and ground (top) for the other pair of electrodes (current, excitation). The surface of
the thorax and the cross-sectional cuts that delimit the computational domain are pre-
sumed electrically insulated (n J 5 0).
Next, an AC problem models a 500-kHz ECM setup. The penetration depth for tis-
p ffiffiffiffiffiffiffiffiffiffiffi
sues with σ B 1-100 mS/m, δ 5 1= μσπf , shows off values larger than the characteris-
tic lengths of the anatomical domains. Table 5.1 presents the electrical properties and the
corresponding penetration for the tissues considered in the model.
The electric field is actually irrotational because the penetration depth exceeds local
length scales of the anatomic regions, hence E 52 rV (complex quantities are
underlined). Using the electric charge conservation law, rUJ 52 jωρ , where
v