Page 167 - Computational Modeling in Biomedical Engineering and Medical Physics

156 Computational Modeling in Biomedical Engineering and Medical Physics

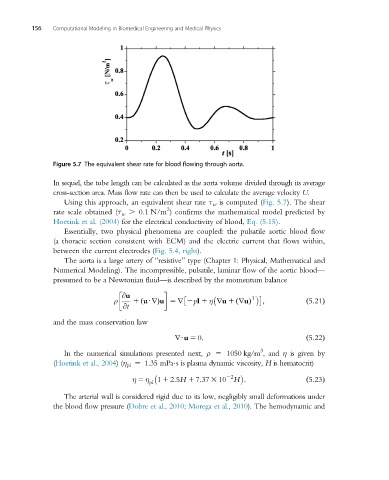
Figure 5.7 The equivalent shear rate for blood flowing through aorta.

In sequel, the tube length can be calculated as the aorta volume divided through its average
cross-section area. Mass flow rate can then be used to calculate the average velocity U.
Using this approach, an equivalent shear rate τ w is computed (Fig. 5.7). The shear
2
rate scale obtained (τ w . 0.1 N/m ) confirms the mathematical model predicted by
Hoetink et al. (2004) for the electrical conductivity of blood, Eq. (5.15).
Essentially, two physical phenomena are coupled: the pulsatile aortic blood flow
(a thoracic section consistent with ECM) and the electric current that flows within,
between the current electrodes (Fig. 5.4, right).
The aorta is a large artery of “resistive” type (Chapter 1: Physical, Mathematical and
Numerical Modeling). The incompressible, pulsatile, laminar flow of the aortic blood—
presumed to be a Newtonian fluid—is described by the momentum balance
@u

ρ 1 uUrÞu 5 r 2pI 1 η ru 1 ruÞ T ; ð5:21Þ
ð
ð
@t
and the mass conservation law
rUu 5 0: ð5:22Þ
3
In the numerical simulations presented next, ρ 5 1050 kg/m ,and η is given by
(Hoetink et al., 2004)(η pl 5 1.35 mPa s is plasma dynamic viscosity, H is hematocrit)

22
η 5 η
1 1 2:5H 1 7:37 3 10 H : ð5:23Þ

pl
The arterial wall is considered rigid due to its low, negligibly small deformations under
the blood flow pressure (Dobre et al., 2010; Morega et al., 2010). The hemodynamic and