Page 299 - Computational Statistics Handbook with MATLAB

288 Computational Statistics Handbook with MATLAB

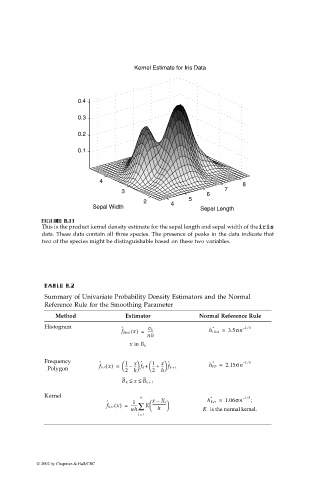
Kernel Estimate for Iris Data

0.4

0.3

0.2

0.1

4
8
3 7
6
2 4 5
Sepal Width Sepal Length

FI F IG URE G 8. RE 8. 1 11 1
U
GU
1
F F II GU RE RE 8. 8. 1 1 1
This is the product kernel density estimate for the sepal length and sepal width of the iris
data. These data contain all three species. The presence of peaks in the data indicate that
two of the species might be distinguishable based on these two variables.

2
..
TA BL L LE L 8 E8 .2 2
2
TA
B
TA
B
B
TA
.
E8
E8
Summary of Univariate Probability Density Estimators and the Normal
Reference Rule for the Smoothing Parameter
Method Estimator Normal Reference Rule
Histogram ⁄
*
ˆ v k h Hist = 3.5σn – 13
f Hist x() = ------
nh
x in B k
Frequency
⁄
*
ˆ 1  x ˆ 1  x ˆ h FP = 2.15σn – 15
-
-
-
-
h 
Polygon f FP x() =  -- – -- f k +  -- + h  1
-- f k +
2
2
B K ≤ x ≤ B k + 1
Kernel n * – 15 ⁄
--------------
ˆ 1  x – X i h Ker = 1.06σn ;
f Ker x() = ------ ∑ K
nh  h  K is the normal kernel.
i = 1
© 2002 by Chapman & Hall/CRC