Page 307 - Computational Statistics Handbook with MATLAB

296 Computational Statistics Handbook with MATLAB

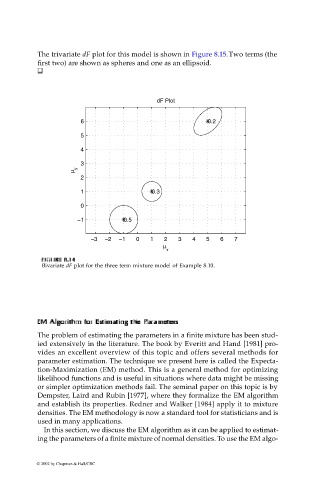
The trivariate dF plot for this model is shown in Figure 8.15. Two terms (the
first two) are shown as spheres and one as an ellipsoid.

dF Plot

6 0.2
5

4
3
µ y
2

1 0.3
0

−1 0.5

−3 −2 −1 0 1 2 3 4 5 6 7
µ
x
IG
FI F U URE G 8.14 RE 8.14
8.14
GU
F F II GU RE RE 8.14
Bivariate dF plot for the three term mixture model of Example 8.10.

gt
gg
thth
g
EAMA
mm aatt
ti inin
th
EEMAMA
EM l ll lggoor rithmithm for for for Esti EEstisti stim ma at nin h e ee Pa ar raamme et teer eerr ss
rss
PPaarr aamm eett
eP
for
ggoorr ithmithm E
The problem of estimating the parameters in a finite mixture has been stud-
ied extensively in the literature. The book by Everitt and Hand [1981] pro-
vides an excellent overview of this topic and offers several methods for
parameter estimation. The technique we present here is called the Expecta-
tion-Maximization (EM) method. This is a general method for optimizing
likelihood functions and is useful in situations where data might be missing
or simpler optimization methods fail. The seminal paper on this topic is by
Dempster, Laird and Rubin [1977], where they formalize the EM algorithm
and establish its properties. Redner and Walker [1984] apply it to mixture
densities. The EM methodology is now a standard tool for statisticians and is
used in many applications.
In this section, we discuss the EM algorithm as it can be applied to estimat-
ing the parameters of a finite mixture of normal densities. To use the EM algo-
© 2002 by Chapman & Hall/CRC