Page 726 - Corrosion Engineering Principles and Practice

678 C h a p t e r 1 5 H i g h - Te m p e r a t u r e C o r r o s i o n 679

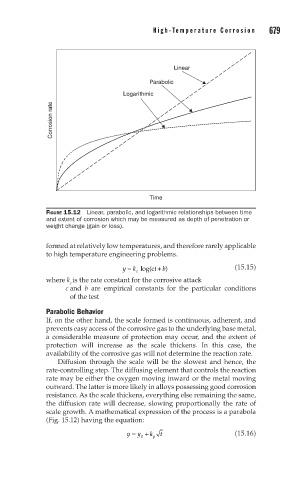
Linear
Parabolic
Logarithmic
Corrosion rate

Time

FIGURE 15.12 Linear, parabolic, and logarithmic relationships between time
and extent of corrosion which may be measured as depth of penetration or
weight change (gain or loss).

formed at relatively low temperatures, and therefore rarely applicable
to high temperature engineering problems.
y = k log(ct + b) (15.15)
e
where k is the rate constant for the corrosive attack
e
c and b are empirical constants for the particular conditions
of the test
Parabolic Behavior
If, on the other hand, the scale formed is continuous, adherent, and
prevents easy access of the corrosive gas to the underlying base metal,
a considerable measure of protection may occur, and the extent of
protection will increase as the scale thickens. In this case, the
availability of the corrosive gas will not determine the reaction rate.
Diffusion through the scale will be the slowest and hence, the
rate-controlling step. The diffusing element that controls the reaction
rate may be either the oxygen moving inward or the metal moving
outward. The latter is more likely in alloys possessing good corrosion
resistance. As the scale thickens, everything else remaining the same,
the diffusion rate will decrease, slowing proportionally the rate of
scale growth. A mathematical expression of the process is a parabola
(Fig. 15.12) having the equation:
y = y + k p t (15.16)
0