Page 287 - DSP Integrated Circuits

272 Chapter 6 DSP Algorithms

6.5 Derive the system of difference equations in computational order for the
filter in Example 4.16
(a) From the filter in Example 4.11, assuming that only every other output
sample is retained.
(b) Directly from
Figure 4.65.
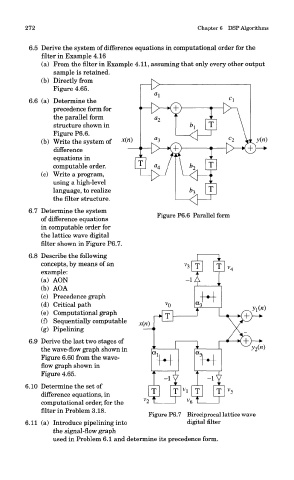
6.6 (a) Determine the
precedence form for
the parallel form
structure shown in
Figure P6.6.
(b) Write the system of
difference
equations in
computable order.
(c) Write a program,
using a high-level
language, to realize
the filter structure.
6.7 Determine the system
of difference equations Figure P6.6 Parallel form
in computable order for
the lattice wave digital
filter shown in Figure P6.7.

6.8 Describe the following
concepts, by means of an
example:
(a) AON
(b) AOA
(c) Precedence graph
(d) Critical path
(e) Computational graph
(f) Sequentially computable
(g) Pipelining
6.9 Derive the last two stages of
the wave-flow graph shown in
Figure 6.60 from the wave-
flow graph shown in
Figure 4.65.

6.10 Determine the set of
difference equations, in
computational order, for the
filter in Problem 3.18.
Figure P6.7 Bireciprocal lattice wave
6.11 (a) Introduce pipelining into digital filter
the signal-flow graph
used in Problem 6.1 and determine its precedence form.