Page 491 - Design for Six Sigma a Roadmap for Product Development

450 Chapter Twelve

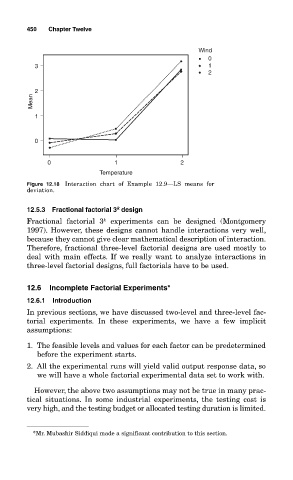
Wind
0
3 1
2

Mean 2

1

0

0 1 2
Temperature
Figure 12.18 Interaction chart of Example 12.9—LS means for
deviation.

k
12.5.3 Fractional factorial 3 design
Fractional factorial 3 experiments can be designed (Montgomery
k
1997). However, these designs cannot handle interactions very well,
because they cannot give clear mathematical description of interaction.
Therefore, fractional three-level factorial designs are used mostly to
deal with main effects. If we really want to analyze interactions in
three-level factorial designs, full factorials have to be used.

12.6 Incomplete Factorial Experiments*
12.6.1 Introduction
In previous sections, we have discussed two-level and three-level fac-
torial experiments. In these experiments, we have a few implicit
assumptions:
1. The feasible levels and values for each factor can be predetermined
before the experiment starts.
2. All the experimental runs will yield valid output response data, so
we will have a whole factorial experimental data set to work with.
However, the above two assumptions may not be true in many prac-
tical situations. In some industrial experiments, the testing cost is
very high, and the testing budget or allocated testing duration is limited.

*Mr. Mubashir Siddiqui made a significant contribution to this section.