Page 451 - Design of Reinforced Masonry Structures

SHEAR WALLS 7.13

Eq. (7.11) is commonly used to determine the relative rigidity. Values of relative rigidi-
ties of walls for various aspect ratios [determined from Eq. (7.11)] are listed in Table A.26.
Note that the relative rigidity is dimensionless quantity (i.e., it has no units), which depends
on only the dimensionless ratio h/d.

7.4.3 Rigidity of a Fixed-Ended Shear Wall
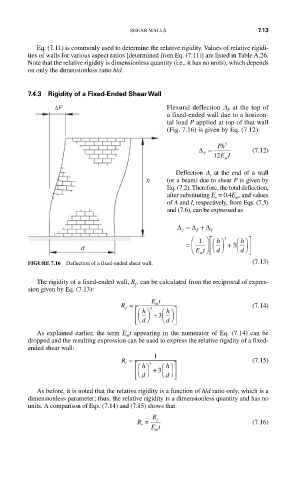
∆F Flexural deflection D at the top of
F
a fixed-ended wall due to a horizon-
tal load P applied at top of that wall
(Fig. 7.16) is given by Eq. (7.12):

∆ = Ph 3 (7.12)
F
12 EI
m
Deflection D at the end of a wall
v
h (or a beam) due to shear P is given by
Eq. (7.2). Therefore, the total deflection,
after substituting E = 0.4E , and values
m
v
of A and I, respectively, from Eqs. (7.5)
and (7.6), can be expressed as
∆ = ∆ + ∆
f F V
⎛ 1 ⎞ ⎛ ⎡ h ⎞ 3 ⎛ h ⎞ ⎤
= ⎜ ⎢ + 3 ⎥
d ⎝ Et ⎟ ⎝ d ⎠ ⎝ d ⎠ ⎦
m ⎠ ⎣
FIGURE 7.16 Deflection of a fixed-ended shear wall. (7.13)

The rigidity of a fixed-ended wall, R , can be calculated from the reciprocal of expres-
f
sion given by Eq. (7.13):
R = Et (7.14)
m
f ⎛ ⎡ h ⎞ 3 ⎛ h ⎞ ⎤
⎢ ⎝ + 3 ⎝ ⎥
⎣ d ⎠ d ⎠ ⎦
As explained earlier, the term E t appearing in the numerator of Eq. (7.14) can be
m
dropped and the resulting expression can be used to express the relative rigidity of a fixed-
ended shear wall:
R = 3 1 h ⎞ ⎤ (7.15)
r
⎢ ⎛ ⎡ ⎝ h ⎞ + 3 ⎛ ⎝ ⎥
⎣ d ⎠ d ⎠ ⎦

As before, it is noted that the relative rigidity is a function of h/d ratio only, which is a
dimensionless parameter; thus, the relative rigidity is a dimensionless quantity and has no
units. A comparison of Eqs. (7.14) and (7.15) shows that
R
R = f (7.16)
r
Et
m