Page 218 - Dynamic Loading and Design of Structures

Page 191

can be expressed in a polar co-ordinate system by a product of a function in z and a function
in r (radial co-ordinate).
Once the velocity potential ( ) is known, the pressure on the surface of the
structure can be calculated from the linearized Bernoulli’s equation ( ) and the
horizontal and vertical forces may be determined by integrating the pressure.
For a vertical cylinder with diameter D=2R, a closed form solution often named the
MacCamy and Fuchs (1954) approach, can be obtained.
The horizontal force q in the x-direction per unit axial length of the cylinder is computed
as:

(5.29)

where , are the
derivatives of first order Bessel functions of the first and second kind, respectively. is the
volume ( )of the cylinder per unit length. The horizontal force may be expressed in terms
of an effective inertia coefficient C and a horizontal water particle acceleration component
M
a at the centre of the section of the cylinder and at an elevation z corresponding to the inertia
x
term of the Morison equation. Hence, ax is given by eqn (5.10). It is noted that the horizontal
wave force is phase-shifted with respect to the acceleration. It is seen that

(5.30)

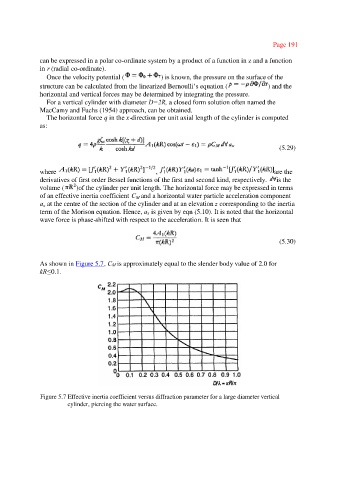
As shown in Figure 5.7, CM is approximately equal to the slender body value of 2.0 for
kR≤0.1.

Figure 5.7 Effective inertia coefficient versus diffraction parameter for a large diameter vertical
cylinder, piercing the water surface.