Page 224 - Dynamic Loading and Design of Structures

Page 197

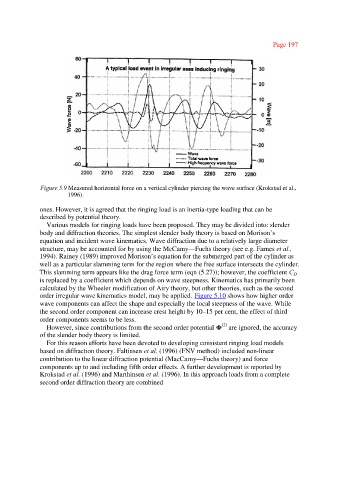
Figure 5.9 Measured horizontal force on a vertical cylinder piercing the wave surface (Krokstad et al.,
1996).

ones. However, it is agreed that the ringing load is an inertia-type loading that can be
described by potential theory.
Various models for ringing loads have been proposed. They may be divided into: slender
body and diffraction theories. The simplest slender body theory is based on Morison’s
equation and incident wave kinematics. Wave diffraction due to a relatively large diameter
structure, may be accounted for by using the McCamy—Fuchs theory (see e.g. Farnes et al.,
1994). Rainey (1989) improved Morison’s equation for the submerged part of the cylinder as
well as a particular slamming term for the region where the free surface intersects the cylinder.
This slamming term appears like the drag force term (eqn (5.27)); however, the coefficient C D
is replaced by a coefficient which depends on wave steepness. Kinematics has primarily been
calculated by the Wheeler modification of Airy theory, but other theories, such as the second
order irregular wave kinematics model, may be applied. Figure 5.10 shows how higher order
wave components can affect the shape and especially the local steepness of the wave. While
the second order component can increase crest height by 10–15 per cent, the effect of third
order components seems to be less.
(2)
However, since contributions from the second order potential Φ are ignored, the accuracy
of the slender body theory is limited.
For this reason efforts have been devoted to developing consistent ringing load models
based on diffraction theory. Faltinsen et al. (1996) (FNV method) included non-linear
contribution to the linear diffraction potential (MacCamy—Fuchs theory) and force
components up to and including fifth order effects. A further development is reported by
Krokstad et al. (1996) and Marthinsen et al. (1996). In this approach loads from a complete
second order diffraction theory are combined