Page 428 - Dynamics of Mechanical Systems

0593_C11_fm Page 409 Monday, May 6, 2002 2:59 PM

Generalized Dynamics: Kinematics and Kinetics 409

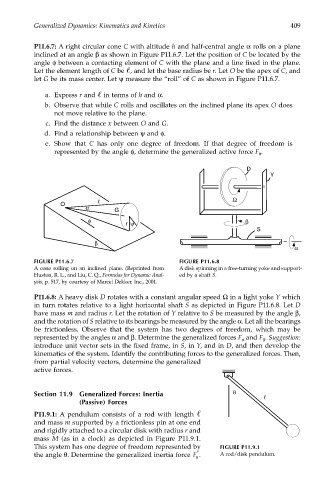
P11.6.7: A right circular cone C with altitude h and half-central angle α rolls on a plane
inclined at an angle β as shown in Figure P11.6.7. Let the position of C be located by the
angle φ between a contacting element of C with the plane and a line fixed in the plane.
Let the element length of C be , and let the base radius be r. Let O be the apex of C, and
let G be its mass center. Let ψ measure the “roll” of C as shown in Figure P11.6.7.

a. Express r and in terms of h and α.
b. Observe that while C rolls and oscillates on the inclined plane its apex O does
not move relative to the plane.
c. Find the distance x between O and G.
d. Find a relationship between ψ and φ.
e. Show that C has only one degree of freedom. If that degree of freedom is
represented by the angle φ, determine the generalized active force F .
θ

D
Y

Ω
O
α G
φ β
r ψ
S
β
α
FIGURE P11.6.7 FIGURE P11.6.8
A cone rolling on an inclined plane. (Reprinted from A disk spinning in a free-turning yoke and support-
Huston, R. L., and Liu, C. Q., Formulas for Dynamic Anal- ed by a shaft S.
ysis, p. 517, by courtesy of Marcel Dekker, Inc., 2001.

P11.6.8: A heavy disk D rotates with a constant angular speed Ω in a light yoke Y which
in turn rotates relative to a light horizontal shaft S as depicted in Figure P11.6.8. Let D
have mass m and radius r. Let the rotation of Y relative to S be measured by the angle β,
and the rotation of S relative to its bearings be measured by the angle α. Let all the bearings
be frictionless. Observe that the system has two degrees of freedom, which may be
represented by the angles α and β. Determine the generalized forces F and F . Suggestion:
β
α
introduce unit vector sets in the fixed frame, in S, in Y, and in D, and then develop the
kinematics of the system. Identify the contributing forces to the generalized forces. Then,
from partial velocity vectors, determine the generalized
active forces.

Section 11.9 Generalized Forces: Inertia θ

(Passive) Forces
P11.9.1: A pendulum consists of a rod with length
and mass m supported by a frictionless pin at one end
and rigidly attached to a circular disk with radius r and
mass M (as in a clock) as depicted in Figure P11.9.1.
This system has one degree of freedom represented by FIGURE P11.9.1
the angle θ. Determine the generalized inertia force F θ * . A rod/disk pendulum.