Page 120 - Academic Press Encyclopedia of Physical Science and Technology 3rd Polymer

P1: FMX/LSU P2: GPB/GRD P3: GLQ Final pages
Encyclopedia of Physical Science and Technology EN012c-593 July 26, 2001 15:56

626 Polymer Processing

cohesionless or cohesive. A cohesionless cluster is formed 2 mm, interfacial tension 30 mN/m, continuous phase vis-
from noninteracting particles or from large particles cosity 100 Pa sec and subjected to a shear rate of 100 sec −1
(>1mm), and its dispersion is determined only by the to- experiences a viscous disruptive stress of 10,000 Pa while
tal deformation of the primary phase. On the other hand, the resisting interfacial tension stress is only 15 Pa.
a cohesive cluster includes interacting particles or very As blending proceeds, the characteristic length of the
small particles, and its dispersion depends on the applied dispersed phase decreases to the point of equilibrium be-
stresses (or equivalently on the deformation rates). In the tween the disruptive hydrodynamic and cohesive interfa-
case of cohesionless clusters, the dispersion is achieved cial tension forces. Of course, during the blending process,
by “peeling off” particles from the surface of the cluster dispersed droplets come in contact with each other and
by tangential velocity components close to the particles. may coalesce, so that coalescence and breakup are two
It is common practice in the polymer processing in- competitive mechanisms in polymer blends. In the final
dustry to make masterbatches or superconcentrates of the blending stages, miscible and immiscible systems behave
dispersed to the continuous phase and thus to increase differently. On the one hand, in miscible systems homog-
the applied stresses by increasing the viscosity. In highly enization is achieved to a very small scale, possibly the
concentrated batches, the viscosity of the medium can be molecular scale, if sufficient time is allowed. On the other
orders of magnitude higher than the viscosity of the poly- hand, immiscible systems exhibit a two-phase structure
mer matrix. For example, the masterbatch of carbon black whose characteristics depend on the physical parameters
in PE contains about 50% carbon black while the final of both polymer phases.
product contains about 2–5% only. The deagglomeration In summary, miscible and immiscible systems show
takes place in the masterbatch where the viscosity is high, similarbehaviorintheinitialstepsofthedispersivemixing
and it is followed by dilution steps in extensive type of process, where hydrodynamic forces deform and disrupt
mixing. the units of the dispersed phase. In the next stages, inter-
Liquid–liquid dispersion is characterized by two facial tension forces come into play and induce motion
phases: the dispersed and the continuous. The physical pa- (interfacial tension driven Rayleigh or capillary distur-
rameters of the two phases affecting a liquid–liquid disper- bances). Then, at the final stages, miscible systems are
sion are viscosity, elasticity, interfacial tension, solubility, expected to be homogenized at the molecular level (if suf-
and diffusion rate. On the basis of solubility, the system is ficient time is allowed), while immiscible systems retain
considered to be miscible, immiscible, or partially misci- the coarser structure of a two-phase system.
ble. Interfacial tension is lowest for miscible systems and As the deformation of the droplets increases, they as-
highest for immiscible systems. All high molecular sub- sume elongated shapes and finally at some value of the
stances have a diffusion coefficient, D, of about 10 −12 to capillary number, called the critical capillary number, Ca c ,
2
10 −14 cm /sec. Consequently, the diffusion rates in molten the disruptive forces exceed the cohesive forces and the
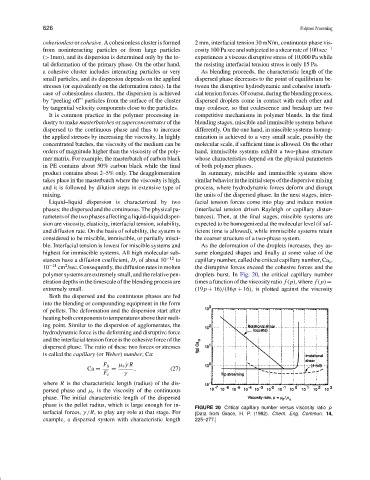
polymer systems are extremely small, and the relative pen- droplets burst. In Fig. 20, the critical capillary number
etration depths in the timescale of the blending process are times a function of the viscosity ratio f (p), where f (p) =
extremely small. (19p + 16)/(16p + 16), is plotted against the viscosity
Both the dispersed and the continuous phases are fed
into the blending or compounding equipment in the form
of pellets. The deformation and the dispersion start after
heatingbothcomponentstotemperaturesabovetheirmelt-
ing point. Similar to the dispersion of agglomerates, the
hydrodynamic force is the deforming and disruptive force
and the interfacial tension force is the cohesive force of the
dispersed phase. The ratio of these two forces or stresses
is called the capillary (or Weber) number, Ca:
µ c ˙γ R
F h
Ca = = , (27)
F c γ
where R is the characteristic length (radius) of the dis-
persed phase and µ c is the viscosity of the continuous
phase. The initial characteristic length of the dispersed
phase is the pellet radius, which is large enough for in-
FIGURE 20 Critical capillary number versus viscosity ratio p.
terfacial forces, γ/R, to play any role at that stage. For [Data from Grace, H. P. (1982). Chem. Eng. Commun. 14,
example, a dispersed system with characteristic length 225–277.]