Page 166 - Entrophy Analysis in Thermal Engineering Systems

Entropy and chemical equilibrium 161

10.5.2 Kinetic model
We now examine the chemical equilibrium of methane steam reforming
using the kinetics of reaction. The rate of reaction at which methane is con-
sumed is determined by [20]

C H 2 O (10.21)
r ¼ κC CH 4
where C is the concentration and κ denotes the reaction constant that is
described in an Arrhenius equation form.

8 15;000 3
κ ¼ 3 10 exp m =kmols (10.22)
T
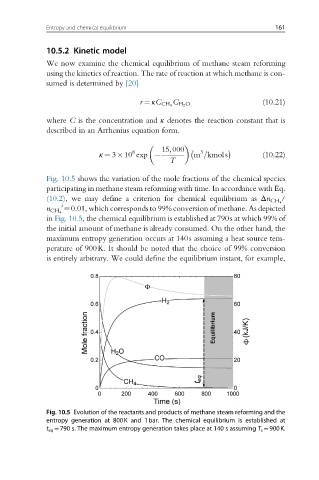
Fig. 10.5 shows the variation of the mole fractions of the chemical species
participating in methane steam reforming with time. In accordance with Eq.
/
(10.2), we may define a criterion for chemical equilibrium as Δn CH 4
¼0.01, which corresponds to 99% conversion of methane. As depicted
i
n CH 4
in Fig. 10.5, the chemical equilibrium is established at 790s at which 99% of
the initial amount of methane is already consumed. On the other hand, the
maximum entropy generation occurs at 140s assuming a heat source tem-
perature of 900K. It should be noted that the choice of 99% conversion
is entirely arbitrary. We could define the equilibrium instant, for example,

Fig. 10.5 Evolution of the reactants and products of methane steam reforming and the
entropy generation at 800K and 1bar. The chemical equilibrium is established at
t eq ¼790 s. The maximum entropy generation takes place at 140 s assuming T s ¼900K.