Page 103 - T. Anderson-Fracture Mechanics - Fundamentals and Applns.-CRC (2005)

1656_C02.fm Page 83 Thursday, April 14, 2005 6:28 PM

Linear Elastic Fracture Mechanics 83

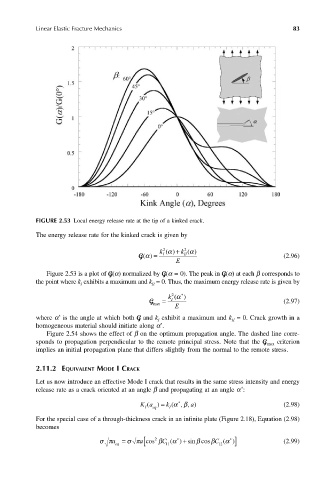
FIGURE 2.53 Local energy release rate at the tip of a kinked crack.
The energy release rate for the kinked crack is given by

k 2 () + k α 2 ()
α
G() = I I I (2.96)
α
E
Figure 2.53 is a plot of G(α) normalized by G(α = 0). The peak in G(α) at each β corresponds to
the point where k exhibits a maximum and k = 0. Thus, the maximum energy release rate is given by
I
II
k 2 (α ∗ )
G = I (2.97)
max E
*
where α is the angle at which both G and k exhibit a maximum and k = 0. Crack growth in a
I
II
*
homogeneous material should initiate along α .
Figure 2.54 shows the effect of β on the optimum propagation angle. The dashed line corre-
sponds to propagation perpendicular to the remote principal stress. Note that the G max criterion
implies an initial propagation plane that differs slightly from the normal to the remote stress.
2.11.2 EQUIVALENT MODE I CRACK

Let us now introduce an effective Mode I crack that results in the same stress intensity and energy
*
release rate as a crack oriented at an angle β and propagating at an angle α :
∗
Ka ) = k (αβ a , ) (2.98)
,
(
q
I
I
e
For the special case of a through-thickness crack in an infinite plate (Figure 2.18), Equation (2.98)
becomes
σπ a eq σπ [ a = 2 β C 11 ( α + ∗ ) β cos β C sin 12 ( α ] cos ∗ ) (2.99)