Page 104 - T. Anderson-Fracture Mechanics - Fundamentals and Applns.-CRC (2005)

1656_C02.fm Page 84 Thursday, April 14, 2005 6:28 PM

84 Fracture Mechanics: Fundamentals and Applications

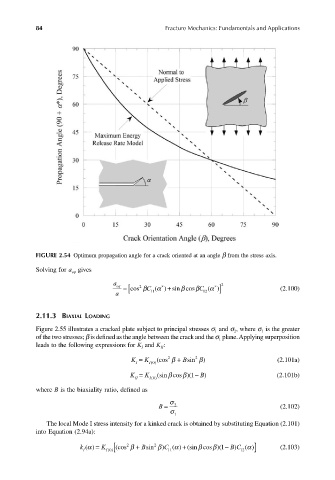
FIGURE 2.54 Optimum propagation angle for a crack oriented at an angle β from the stress axis.

Solving for a gives
eq
a eq 2 ∗ +[ ∗ 2
β
a = C 11 ) sin cosβ C (α 12 ( α ) ] cos β (2.100)

2.11.3 BIAXIAL LOADING

Figure 2.55 illustrates a cracked plate subject to principal stresses σ and σ , where σ is the greater
1
1
2
of the two stresses; β is defined as the angle between the crack and the σ plane. Applying superposition
1
leads to the following expressions for K and K :
II
I
K I K = I () (cos β 2 B + sin β 2 ) (2.101a)
0
β
K II K = I() (sin cos )(1 B − ) (2.101b)
β
0
where B is the biaxiality ratio, defined as
σ
B = 2 (2.102)
σ
1
The local Mode I stress intensity for a kinked crack is obtained by substituting Equation (2.101)
into Equation (2.94a):
k I α K ( ) = I ()[ 0 (cos β 2 B 2 ) Csin β 11 ( ) (sin cos 1 B )( − ) C β 12 ( )] α (2.103)
α+
+
β