Page 162 - T. Anderson-Fracture Mechanics - Fundamentals and Applns.-CRC (2005)

1656_C003.fm Page 142 Monday, May 23, 2005 5:42 PM

142 Fracture Mechanics: Fundamentals and Applications

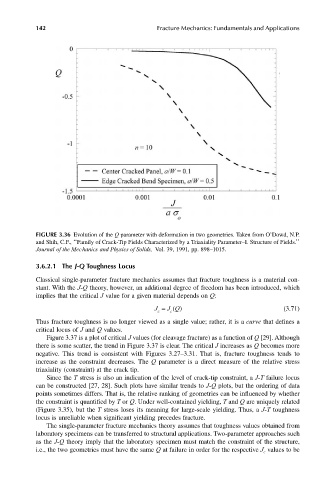
FIGURE 3.36 Evolution of the Q parameter with deformation in two geometries. Taken from O’Dowd, N.P.
and Shih, C.F., ‘‘Family of Crack-Tip Fields Characterized by a Triaxiality Parameter–I. Structure of Fields.’’
Journal of the Mechanics and Physics of Solids, Vol. 39, 1991, pp. 898–1015.

3.6.2.1 The J-Q Toughness Locus
Classical single-parameter fracture mechanics assumes that fracture toughness is a material con-
stant. With the J-Q theory, however, an additional degree of freedom has been introduced, which
implies that the critical J value for a given material depends on Q:
Q
J c J = c () (3.71)
Thus fracture toughness is no longer viewed as a single value; rather, it is a curve that defines a
critical locus of J and Q values.
Figure 3.37 is a plot of critical J values (for cleavage fracture) as a function of Q [29]. Although
there is some scatter, the trend in Figure 3.37 is clear. The critical J increases as Q becomes more
negative. This trend is consistent with Figures 3.27–3.31. That is, fracture toughness tends to
increase as the constraint decreases. The Q parameter is a direct measure of the relative stress
triaxiality (constraint) at the crack tip.
Since the T stress is also an indication of the level of crack-tip constraint, a J-T failure locus
can be constructed [27, 28]. Such plots have similar trends to J-Q plots, but the ordering of data
points sometimes differs. That is, the relative ranking of geometries can be influenced by whether
the constraint is quantified by T or Q. Under well-contained yielding, T and Q are uniquely related
(Figure 3.35), but the T stress loses its meaning for large-scale yielding. Thus, a J-T toughness
locus is unreliable when significant yielding precedes fracture.
The single-parameter fracture mechanics theory assumes that toughness values obtained from
laboratory specimens can be transferred to structural applications. Two-parameter approaches such
as the J-Q theory imply that the laboratory specimen must match the constraint of the structure,
i.e., the two geometries must have the same Q at failure in order for the respective J values to be
c