Page 165 - T. Anderson-Fracture Mechanics - Fundamentals and Applns.-CRC (2005)

1656_C003.fm Page 145 Monday, May 23, 2005 5:42 PM

Elastic-Plastic Fracture Mechanics 145

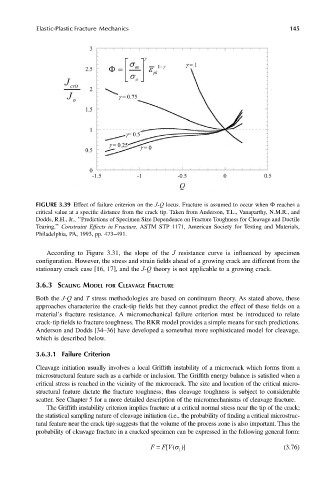
FIGURE 3.39 Effect of failure criterion on the J-Q locus. Fracture is assumed to occur when Φ reaches a
critical value at a specific distance from the crack tip. Taken from Anderson, T.L., Vanaparthy, N.M.R., and
Dodds, R.H., Jr., ‘‘Predictions of Specimen Size Dependence on Fracture Toughness for Cleavage and Ductile
Tearing.’’ Constraint Effects in Fracture, ASTM STP 1171, American Society for Testing and Materials,
Philadelphia, PA, 1993, pp. 473–491.

According to Figure 3.31, the slope of the J resistance curve is influenced by specimen
configuration. However, the stress and strain fields ahead of a growing crack are different from the
stationary crack case [16, 17], and the J-Q theory is not applicable to a growing crack.

3.6.3 SCALING MODEL FOR CLEAVAGE FRACTURE
Both the J-Q and T stress methodologies are based on continuum theory. As stated above, these
approaches characterize the crack-tip fields but they cannot predict the effect of these fields on a
material’s fracture resistance. A micromechanical failure criterion must be introduced to relate
crack-tip fields to fracture toughness. The RKR model provides a simple means for such predictions.
Anderson and Dodds [34–36] have developed a somewhat more sophisticated model for cleavage,
which is described below.
3.6.3.1 Failure Criterion

Cleavage initiation usually involves a local Griffith instability of a microcrack which forms from a
microstructural feature such as a carbide or inclusion. The Griffith energy balance is satisfied when a
critical stress is reached in the vicinity of the microcrack. The size and location of the critical micro-
structural feature dictate the fracture toughness; thus cleavage toughness is subject to considerable
scatter. See Chapter 5 for a more detailed description of the micromechanisms of cleavage fracture.
The Griffith instability criterion implies fracture at a critical normal stress near the tip of the crack;
the statistical sampling nature of cleavage initiation (i.e., the probability of finding a critical microstruc-
tural feature near the crack tip) suggests that the volume of the process zone is also important. Thus the
probability of cleavage fracture in a cracked specimen can be expressed in the following general form:

σ
V
F F = [( )] (3.76)
1