Page 271 - Fundamentals of Reservoir Engineering
P. 271
OILWELL TESTING 208
and subtracting equ. (7.66), the equation of the linear buildup, from this equation gives
t +∆ t
−
0.0288 = (p ws (LIN ) p ws = In t -In t ∆ DA − ln + p D (MBH ) ( t ∆ DA )
DA
t ∆
which can be simplified as
t +∆ t
0.0288 ∆ p ws = p DMBH ) (∆ t DA ) − ln (7.68)
(
t ∆
in which ∆p ws = p ws(LIN) − p ws, the pressure deviation below the linear buildup trend.
Values of ∆p ws as a function of ∆t are listed in table 7.9 for the three geometrical
configurations presented in table 7.8. The actual pressure buildups for these three
cases are included in fig. 7.26 by plotting the deviations ∆p ws below the linear buildups.
2 4
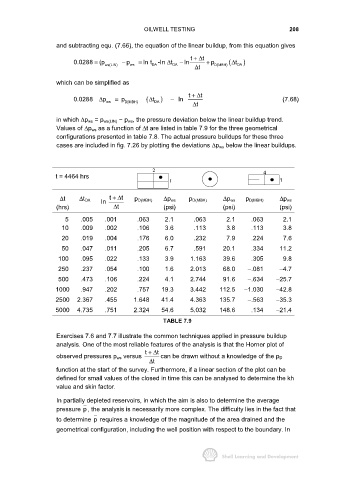
t = 4464 hrs
1 1
∆t ∆t DA ln t +∆ t p D(MBH) ∆p ws p D(MBH) ∆p ws p D(MBH) ∆p ws
(hrs) t ∆ (psi) (psi) (psi)
5 .005 .001 .063 2.1 .063 2.1 .063 2.1
10 .009 .002 .106 3.6 .113 3.8 .113 3.8
20 .019 .004 .176 6.0 .232 7.9 .224 7.6
50 .047 .011 .205 6.7 .591 20.1 .334 11.2
100 .095 .022 .133 3.9 1.163 39.6 .305 9.8
250 .237 .054 .100 1.6 2.013 68.0 −.081 −4.7
500 .473 .106 .224 4.1 2.744 91.6 −.634 −25.7
1000 .947 .202 .757 19.3 3.442 112.5 −1.030 −42.8
2500 2.367 .455 1.648 41.4 4.363 135.7 −.563 −35.3
5000 4.735 .751 2.324 54.6 5.032 148.6 .134 −21.4
TABLE 7.9
Exercises 7.6 and 7.7 illustrate the common techniques applied in pressure buildup
analysis. One of the most reliable features of the analysis is that the Horner plot of
t +∆ t
observed pressures p ws versus can be drawn without a knowledge of the p D
t ∆
function at the start of the survey. Furthermore, if a linear section of the plot can be
defined for small values of the closed in time this can be analysed to determine the kh
value and skin factor.
In partially depleted reservoirs, in which the aim is also to determine the average
pressure p, the analysis is necessarily more complex. The difficulty lies in the fact that
to determine p requires a knowledge of the magnitude of the area drained and the
geometrical configuration, including the well position with respect to the boundary. In