Page 519 - Fundamentals of Water Treatment Unit Processes : Physical, Chemical, and Biological

474 Fundamentals of Water Treatment Unit Processes: Physical, Chemical, and Biological

0 C C 0
BOX 15.2 REVIEW OF SALIENT POINTS
ABOUT PACKED-BED REACTORS
Z
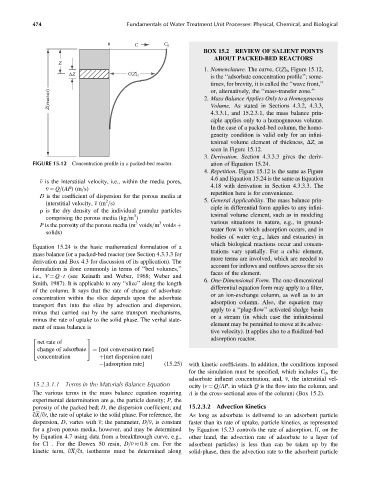
1. Nomenclature. The curve, C(Z) t , Figure 15.12,
ΔZ C(Z) t is the ‘‘adsorbate concentration profile’’; some-
times, for brevity, it is called the ‘‘wave front,’’
or, alternatively, the ‘‘mass-transfer zone.’’
Z(reactor) 2. Mass Balance Applies Only to a Homogeneous
Volume. As stated in Sections 4.3.2, 4.3.3,
4.3.3.1, and 15.2.3.1, the mass balance prin-
ciple applies only to a homogeneous volume.
In the case of a packed-bed column, the homo-
geneity condition is valid only for an infini-
tesimal volume element of thickness, DZ,as
seen in Figure 15.12.
3. Derivation. Section 4.3.3.3 gives the deriv-
FIGURE 15.12 Concentration profile in a packed-bed reactor. ation of Equation 15.24.
4. Repetition. Figure 15.12 is the same as Figure
4.6 and Equation 15.24 is the same as Equation
v is the interstitial velocity, i.e., within the media pores,
4.18 with derivation in Section 4.3.3.3. The
v ¼ Q=(AP)(m=s)
repetition here is for convenience.
D is the coefficient of dispersion for the porous media at
2
interstitial velocity, v (m =s) 5. General Applicability. The mass balance prin-
ciple in differential form applies to any infini-
r is the dry density of the individual granular particles
3
comprising the porous media (kg=m ) tesimal volume element, such as in modeling
3 3 various situations in nature, e.g., in ground-
water flow in which adsorption occurs, and in
P is the porosity of the porous media (m voids=m voids þ
solids)
bodies of water (e.g., lakes and estuaries) in
which biological reactions occur and concen-
Equation 15.24 is the basic mathematical formulation of a
trations vary spatially. For a cubic element,
mass balance for a packed-bed reactor (see Section 4.3.3.3 for
more terms are involved, which are needed to
derivation and Box 4.3 for discussion of its application). The
account for inflows and outflows across the six
formulation is done commonly in terms of ‘‘bed volumes,’’
faces of the element.
i.e., V ¼ Q t (see Keinath and Weber, 1968; Weber and
6. One-Dimensional Form. The one-dimensional
Smith, 1987). It is applicable to any ‘‘slice’’ along the length
differential equation form may apply to a filter,
of the column. It says that the rate of change of adsorbate
or an ion-exchange column, as well as to an
concentration within the slice depends upon the adsorbate
adsorption column. Also, the equation may
transport flux into the slice by advection and dispersion,
apply to a ‘‘plug-flow’’ activated sludge basin
minus that carried out by the same transport mechanisms,
or a stream (in which case the infinitesimal
minus the rate of uptake to the solid phase. The verbal state-
element may be permitted to move at its advec-
ment of mass balance is
tive velocity). It applies also to a fluidized-bed
2 3 adsorption reactor.
net rate of
5
4 change of adsorbate ¼ [net conversation rate]
concentration þ[net dispersion rate]
[adsorption rate] (15:25) with kinetic coefficients. In addition, the conditions imposed
for the simulation must be specified, which includes C 0 , the
adsorbate influent concentration; and, v, the interstitial vel-
15.2.3.1.1 Terms in the Materials Balance Equation ocity (v ¼ Q=AP, in which Q is the flow into the column, and
The various terms in the mass balance equation requiring A is the cross-sectional area of the column) (Box 15.2).
experimental determination are r, the particle density; P, the
porosity of the packed bed; D, the dispersion coefficient; and 15.2.3.2 Advection Kinetics
qX=qt, the rate of uptake to the solid phase. For reference, the As long as adsorbate is delivered to an adsorbent particle
dispersion, D, varies with v; the parameter, D=v, is constant faster than its rate of uptake, particle kinetics, as represented
for a given porous media, however, and may be determined by Equation 15.23 controls the rate of adsorption. If, on the
by Equation 4.7 using data from a breakthrough curve, e.g., other hand, the advection rate of adsorbate to a layer (of
for Cl . For the Dowex 50 resin, D=v 0.8 cm. For the adsorbent particles) is less than can be taken up by the

kinetic term, qX=qt, isotherms must be determined along solid-phase, then the advection rate to the adsorbent particle