Page 265 - gas transport in porous media

262
Šolcová and Schneider
2.8
600 3.0
2.6
2.4
∆P (Pa) 2.2 log (∆P/Pa)
400
2.0
200
1.8
1.6
0 1.4
0 200 400
t (s)

o
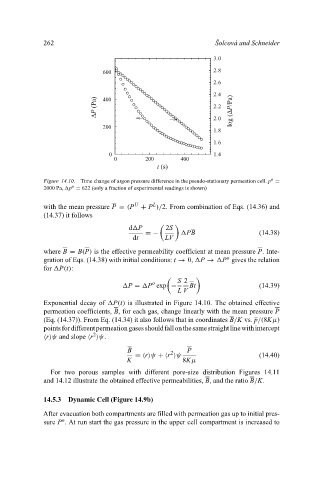
Figure 14.10. Time change of argon pressure difference in the pseudo-stationary permeation cell. p =
o
2000 Pa, p = 622 (only a fraction of experimental readings is shown)
L
U
with the mean pressure P = (P + P )/2. From combination of Eqs. (14.36) and
(14.37) it follows

d P 2S
=− PB (14.38)
dt LV
where B = B(P) is the effective permeability coefficient at mean pressure P. Inte-
o
gration of Eqs. (14.38) with initial conditions: t → 0, P → P gives the relation
for P(t):

S 2
o
P = P exp − Bt (14.39)
L V
Exponential decay of P(t) is illustrated in Figure 14.10. The obtained effective
permeation coefficients, B, for each gas, change linearly with the mean pressure P
(Eq. (14.37)). From Eq. (14.34) it also follows that in coordinates B/K vs. p/(8Kµ)
pointsfordifferentpermeationgasesshouldfallonthesamestraightlinewithintercept
2
r ψ and slope r ψ.
B 2 P
= r ψ + r ψ (14.40)
K 8Kµ
For two porous samples with different pore-size distribution Figures 14.11
and 14.12 illustrate the obtained effective permeabilities, B, and the ratio B/K.

14.5.3 Dynamic Cell (Figure 14.9b)
After evacuation both compartments are filled with permeation gas up to initial pres-
o
sure P . At run start the gas pressure in the upper cell compartment is increased to