Page 260 - gas transport in porous media

Chapter 14: Experimental Determination of Transport Parameters
3 2 1 257

c/c max

0 10 20 0

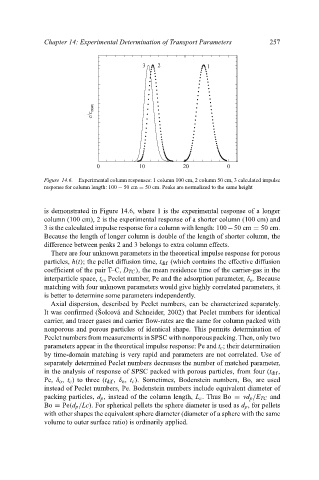
Figure 14.6. Experimental column responses: 1 column 100 cm, 2 column 50 cm, 3 calculated impulse
response for column length: 100 − 50 cm = 50 cm. Peaks are normalized to the same height

is demonstrated in Figure 14.6, where 1 is the experimental response of a longer
column (100 cm), 2 is the experimental response of a shorter column (100 cm) and
3 is the calculated impulse response for a column with length: 100−50 cm = 50 cm.
Because the length of longer column is double of the length of shorter column, the
difference between peaks 2 and 3 belongs to extra column effects.
There are four unknown parameters in the theoretical impulse response for porous
particles, h(t); the pellet diffusion time, t dif (which contains the effective diffusion
coefficient of the pair T–C, D TC ), the mean residence time of the carrier-gas in the
interparticle space, t c , Peclet number, Pe and the adsorption parameter, δ o . Because
matching with four unknown parameters would give highly correlated parameters, it
is better to determine some parameters independently.
Axial dispersion, described by Peclet numbers, can be characterized separately.
It was confirmed (Šolcová and Schneider, 2002) that Peclet numbers for identical
carrier, and tracer gases and carrier flow-rates are the same for column packed with
nonporous and porous particles of identical shape. This permits determination of
Peclet numbers from measurements in SPSC with nonporous packing. Then, only two
parameters appear in the theoretical impulse response: Pe and t c ; their determination
by time-domain matching is very rapid and parameters are not correlated. Use of
separately determined Peclet numbers decreases the number of matched parameter,
in the analysis of response of SPSC packed with porous particles, from four (t dif ,
Pe, δ o , t c ) to three (t dif , δ o , t c ). Sometimes, Bodenstein numbers, Bo, are used
instead of Peclet numbers, Pe. Bodenstein numbers include equivalent diameter of
packing particles, d p , instead of the column length, L c . Thus Bo = vd p /E TC and
Bo = Pe(d p /Lc). For spherical pellets the sphere diameter is used as d p , for pellets
with other shapes the equivalent sphere diameter (diameter of a sphere with the same
volume to outer surface ratio) is ordinarily applied.