Page 261 - gas transport in porous media

258
1
10 1 Šolcová and Schneider
10

Bo

10 0 10 0

10 0 10 1 10 2 10 1 10 2
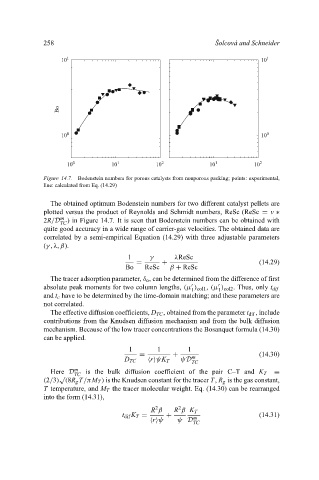
Figure 14.7. Bodenstein numbers for porous catalysts from nonporous packing; points: experimental,
line: calculated from Eq. (14.29)

The obtained optimum Bodenstein numbers for two different catalyst pellets are
plotted versus the product of Reynolds and Schmidt numbers, ReSc (ReSc = v ∗
m
2R/D ) in Figure 14.7. It is seen that Bodenstein numbers can be obtained with
TC
quite good accuracy in a wide range of carrier-gas velocities. The obtained data are
correlated by a semi-empirical Equation (14.29) with three adjustable parameters
(γ , λ, β).
1 γ λReSc
= + (14.29)
Bo ReSc β + ReSc
The tracer adsorption parameter, δ o , can be determined from the difference of first

absolute peak moments for two column lengths, (µ ) col1 , (µ ) col2 . Thus, only t dif
1 1
and t c have to be determined by the time-domain matching; and these parameters are
not correlated.
The effective diffusion coefficients, D TC , obtained from the parameter t dif , include
contributions from the Knudsen diffusion mechanism and from the bulk diffusion
mechanism. Because of the low tracer concentrations the Bosanquet formula (14.30)
can be applied.
1 1 1
= + m (14.30)
D TC r ψK T ψD
TC
m
Here D TC is the bulk diffusion coefficient of the pair C–T and K T ≡
√
(2/3) (8R g T/πM T ) is the Knudsen constant for the tracer T, R g is the gas constant,
T temperature, and M T the tracer molecular weight. Eq. (14.30) can be rearranged
into the form (14.31),
2
2
R β R β K T
t dif K T = + m (14.31)
r ψ ψ D
TC