Page 56 - Geochemical Remote Sensing of The Sub-Surface

Geoelectrochemistry and stream dispersion 33

U, ~g/l
80
70

60
50

40
30

20
10

0 ....... t ,, l I . . . . . ~ ~ ......
0 20 40 60 80 100 120
min
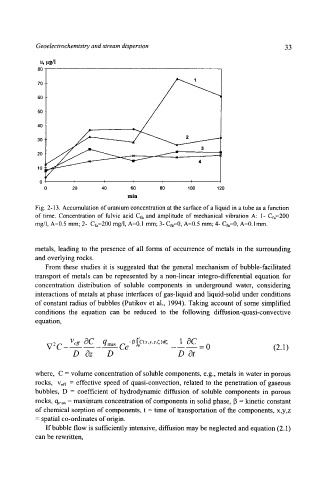
Fig. 2-13. Accumulation of uranium concentration at the surface of a liquid in a tube as a function
of time. Concentration of fulvic acid Cfa and amplitude of mechanical vibration A: 1- Era=200
rag/I, A=0.5 mm; 2- Cf~=200 mg/1, A=0.1 mm; 3- Cfa=0, A=0.5 mm; 4- Cfa=0, A=0. l mm.

metals, leading to the presence of all forms of occurrence of metals in the surrounding
and overlying rocks.
From these studies it is suggested that the general mechanism of bubble-facilitated
transport of metals can be represented by a non-linear integro-differential equation for
concentration distribution of soluble components in underground water, considering
interactions of metals at phase interfaces of gas-liquid and liquid-solid under conditions
of constant radius of bubbles (Putikov et al., 1994). Taking account of some simplified
conditions the equation can be reduced to the following diffusion-quasi-convective
equation,

V 2 C ]2eft #C q max Ce -[~ [tCJo (x,y,z,~)d~ _ u ~ l C = 0 (2.1)
a
D Oz D Dat

where, C - volume concentration of soluble components, e.g., metals in water in porous
rocks, veff = effective speed of quasi-convection, related to the penetration of gaseous
bubbles, D = coefficient of hydrodynamic diffusion of soluble components in porous
rocks, qm~x = maximum concentration of components in solid phase, 13 = kinetic constant
of chemical sorption of components, t = time of transportation of the components, x,y,z
- spatial co-ordinates of origin.
If bubble flow is sufficiently intensive, diffusion may be neglected and equation (2.1)
can be rewritten,