Page 219 - Geometric Modeling and Algebraic Geometry

222 M. Shalaby and B. J¨ uttler
Algorithm 3 Approximate implicitization by approximately orthogonal surfaces
Input A parametric space curve C or a set of sampled points p i.
Output An approximate implicit representation as the intersection of two approximately or-
thogonal surfaces.
1: Run Steps 1, 2, 3 of Algorithm 2.
¯
g
2: Approximate ∇f and ∇g by polynomials or piecewise polynomials f and ¯ by
minimizing (12.11).
3: Introduce the two auxiliary function F and G as in (12.9) and (12.10), where the norms
of the gradients are replaced by their piecewise polynomial approximants.
4: Represent the given curve as the intersection of the two approximately orthogonal alge-
braic surfaces F, G.

1.2 1.2
1 1
0.8 0.8
z z
0.6 0.6
0.4 0.4
0.2 0.2
0 0
0.2 0.2
0.4 0.4
0.6 1.2 0.6 1.2
x 1 x 1
0.8 0.8 0.8 0.8
0.6 0.6
1 0.4 y 1 0.4 y
0.2 0.2
1.2 0 1.2 0
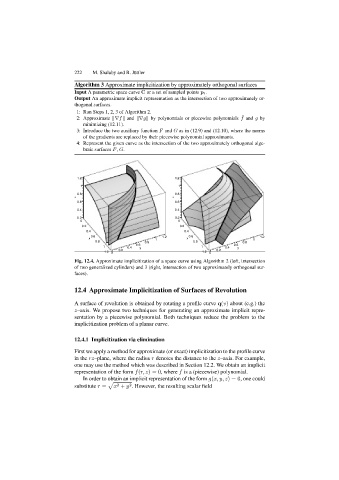
Fig. 12.4. Approximate implicitization of a space curve using Algorithm 2 (left, intersection
of two generalized cylinders) and 3 (right, intersection of two approximately orthogonal sur-
faces).
12.4 Approximate Implicitization of Surfaces of Revolution

A surface of revolution is obtained by rotating a profile curve q(v) about (e.g.) the
z–axis. We propose two techniques for generating an approximate implicit repre-
sentation by a piecewise polynomial. Both techniques reduce the problem to the
implicitization problem of a planar curve.

12.4.1 Implicitization via elimination
First we apply a method for approximate (or exact) implicitization to the profile curve
in the rz–plane, where the radius r denotes the distance to the z–axis. For example,
one may use the method which was described in Section 12.2. We obtain an implicit
representation of the form f(r, z)=0, where f is a (piecewise) polynomial.
In order to obtain an implicit representation of the form g(x, y, z)=0, one could
&
substitute r = x + y . However, the resulting scalar field
2
2