Page 787 - Handbook Of Integral Equations

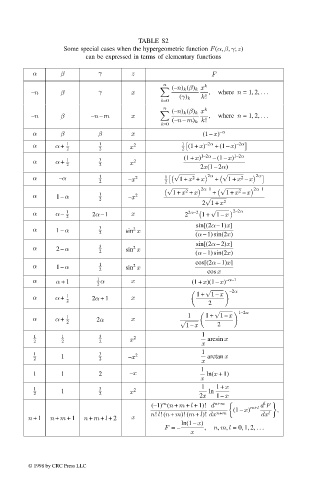
TABLE S2
Some special cases when the hypergeometric function F(α, β, γ; z)
can be expressed in terms of elementary functions

α β γ z F
n k
(–n) k (β) k x
–n β γ x , where n =1, 2, ...
(γ) k k!
k=0
n k
(–n) k (β) k x
–n β –n – m x , where n =1, 2, ...
(–n – m) k k!
k=0
α β β x (1 – x) –α
α α + 1 1 x 2 1 (1 + x) –2α +(1 – x) –2α
2 2 2
(1 + x) 1–2α – (1 – x) 1–2α
α α + 1 3 x 2
2 2
2x(1 – 2α)
√ 2α √
2α
α –α 1 –x 2 1 1+ x + x + 1+ x – x
2
2
2 2
√ 2α–1 √ 2α–1
2
2
1+ x + x + 1+ x – x
1
α 1 – α –x 2 √
2
2 1+ x 2
√ 2–2α

α α – 1 2α – 1 x 2 2α–2 1+ 1 – x
2
sin[(2α – 1)x]
α 1 – α 3 sin x
2
2 (α – 1) sin(2x)
sin[(2α – 2)x]
α 2 – α 3 2 sin x
2
(α – 1) sin(2x)
cos[(2α – 1)x]
2
α 1 – α 1 sin x
2
cos x
α α +1 1 α x (1 + x)(1 – x) –α–1
2
√
1+ 1 – x –2α
α α + 1 2α +1 x
2
2
√
1 – x 1–2α
α α + 1 2α x √ 1 1+
2
1 – x 2
1
1 1 3 2
2 2 2 x arcsin x
x
1
1 3 2
2 1 2 –x arctan x
x
1
1 1 2 –x ln(x +1)
x
1 1+ x
1 3 2
2 1 2 x ln
2x 1 – x
m
l
(–1) (n + m + l + 1)! d n+m m+l d F
(1 – x) ,
n! l!(n + m)! (m + l)! dx n+m dx l
n +1 n + m +1 n + m + l +2 x
ln(1 – x)
F = – , n, m, l = 0,1,2, ...
x
© 1998 by CRC Press LLC
© 1998 by CRC Press LLC
Page 772