Page 594 - Handbook of Battery Materials

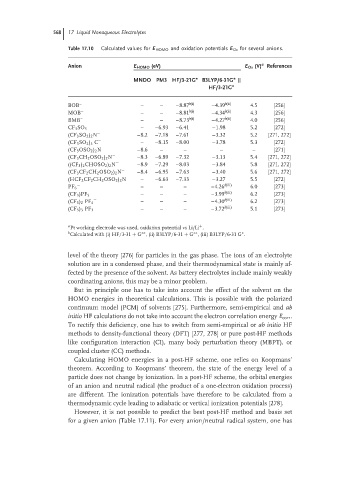
568 17 Liquid Nonaqueous Electrolytes

Table 17.10 Calculated values for E HOMO and oxidation potentials E Ox for several anions.

a
Anion E HOMO (eV) E Ox (V) References
∗
MNDO PM3 HF/3-21G ∗ B3LYP/6-31G ||
HF/3-21G ∗
BOB – – – –8.87 b(i) –4.39 b(ii) 4.5 [256]
MOB – – – –8.81 b(i) –4.34 b(ii) 4.3 [256]
BMB – – – –8.73 b(i) –4.27 b(ii) 4.0 [256]
− – –6.93 –6.41 –1.98 5.2 [272]
CF 3 SO 3
(CF 3 SO 2 ) 2 N − –8.2 –7.18 –7.61 –3.32 5.2 [271, 272]
(CF 3 SO 2 ) 3 C − – –8.15 –8.00 –3.78 5.3 [272]
(CF 3 OSO 2 ) 2 N − –8.6 – – – – [271]
(CF 3 CH 2 OSO 2 ) 2 N − –8.3 –6.89 –7.32 –3.13 5.4 [271, 272]
((CF 3 ) 2 CHOSO 2 ) 2 N − –8.9 –7.29 –8.03 –3.84 5.8 [271, 272]
(CF 3 CF 2 CH 2 OSO 2 ) 2 N − –8.4 –6.95 –7.63 –3.40 5.6 [271, 272]
(HCF 2 CF 2 CH 2 OSO 2 ) 2 N − – –6.63 –7.33 –3.27 5.5 [272]
− b(iii)
PF 6 – – – –4.26 6.0 [273]
− – – – –3.99 b(iii) 6.2 [273]
(CF 3 )PF 5
− b(iii)
(CF 3 ) 2 PF 4 – – – –4.30 6.2 [273]
− – – – –3.72 b(iii) 5.1 [273]
(CF 3 ) 3 PF 3
a Pt working electrode was used, oxidation potential vs Li/Li .
+
b ∗∗ ∗∗ ∗
Calculated with (i) HF/3-31 + G , (ii) B3LYP/6-31 + G , (iii) B3LYP/6-31 G .
level of the theory [276] for particles in the gas phase. The ions of an electrolyte
solution are in a condensed phase, and their thermodynamical state is mainly af-
fected by the presence of the solvent. As battery electrolytes include mainly weakly
coordinating anions, this may be a minor problem.
But in principle one has to take into account the effect of the solvent on the
HOMO energies in theoretical calculations. This is possible with the polarized
continuum model (PCM) of solvents [275]. Furthermore, semi-empirical and ab
initio HF calculations do not take into account the electron correlation energy E corr .
To rectify this deficiency, one has to switch from semi-empirical or ab initio HF
methods to density-functional theory (DFT) [277, 278] or pure post-HF methods
like configuration interaction (CI), many body perturbation theory (MBPT), or
coupled cluster (CC) methods.
Calculating HOMO energies in a post-HF scheme, one relies on Koopmans’
theorem. According to Koopmans’ theorem, the state of the energy level of a
particle does not change by ionization. In a post-HF scheme, the orbital energies
of an anion and neutral radical (the product of a one-electron oxidation process)
are different. The ionization potentials have therefore to be calculated from a
thermodynamic cycle leading to adiabatic or vertical ionization potentials [278].
However, it is not possible to predict the best post-HF method and basis set
for a given anion (Table 17.11). For every anion/neutral radical system, one has