Page 196 - Hydrogeology Principles and Practice

HYDC05 12/5/05 5:35 PM Page 179

Groundwater investigation techniques 179

BO X
Continued
5.2

Fig. 2 Diagram showing the match point
found from the overlay of a type curve
(Theis curve, Fig. 5.33) to the field curve
for the constant discharge pumping test
data obtained for Woolhampton river
regulation borehole (Table 1).

match point, four values are obtained which define W(u), 1/u, s 3.5
•
and t. For Woolhampton, the four match point values are: W(u) = 1;
1/u = 1; s = 1.5 m; t = 2600 s. Hence, rearranging equation 5.36, 3.0
and being careful to work in a consistent set of units (here in metres
and seconds), a value for the Chalk aquifer transmissivity is found 2.5 • • •
from: Residual drawdown, s′(m) 2.0 • • •
. 10
=
=
T Q Wu() 60 × 3 1.5 • • • • • 2.3
×
×
6
s4p 1 . ,400 • •
8
4
× p
5
2 −1
2
= 0.003684 m s or 318 m day −1 eq. 1 1.0 • • •
• t/t ′ = 1 cycle
0.5 • • • •
and using equation 5.35, a value for the confined Chalk storage • • •
coefficient is found from: 0
0.1 1 Time ratio, t/t′ 10 100
×
×
4
× 4
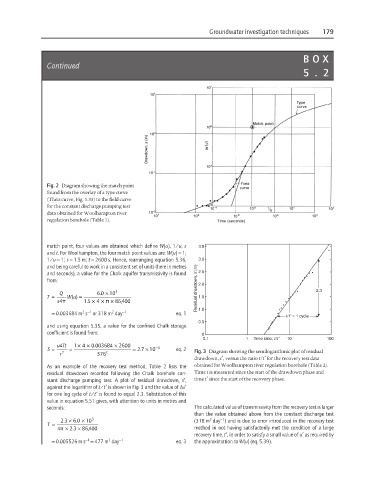
S = uTt 1 . 0 003684 2600 . 10 −4 eq. 2 Fig. 3 Diagram showing the semilogarithmic plot of residual
=
×
= 27
r 2 376 2
drawdown, s′, versus the ratio t/t′ for the recovery test data
As an example of the recovery test method, Table 2 lists the obtained for Woolhampton river regulation borehole (Table 2).
residual drawdown recorded following the Chalk borehole con- Time t is measured since the start of the drawdown phase and
stant discharge pumping test. A plot of residual drawdown, s′, time t′ since the start of the recovery phase.
against the logarithm of t/t′ is shown in Fig. 3 and the value of ∆s′
for one log cycle of t/t′ is found to equal 2.3. Substitution of this
value in equation 5.51 gives, with attention to units in metres and
seconds: The calculated value of transmissivity from the recovery test is larger
than the value obtained above from the constant discharge test
2
−1
. . 10
=
T 23 × 60 × 3 (318 m day ) and is due to error introduced in the recovery test
×
×
3
2
4p . ,400 method in not having satisfactorily met the condition of a large
6
8
recovery time, t′, in order to satisfy a small value of u′ as required by
−1
2
= 0.005526 m s = 477 m day −1 eq. 3 the approximation to W(u) (eq. 5.39).